
物理学对于多因素(多变量)的问题常常采用控制因素(变量)的办法,即把多因素的问题转变为多个单因素的问题,分别加以研究,最后再综和解决,这种方法叫控制变量法。
例题:(2008年广东)伽利略在著名的斜面实验中,让小球分别沿倾角不同、阻力很小的斜面从静止开始滚下,他通过实验观察和逻辑推理,得到的正确结论有( )
A.倾角一定时,小球在斜面上的位移与时间成正比
B.倾角一定时,小球在斜面上的速度与时间成正比
C.斜面长度一定时,小球从顶端滚到底端时的速度与倾角无关
D.斜面长度一定时,小球从顶端滚到底端所需的时间与倾角无关
解析:倾角一定时,小球在斜面上的位移与时间的平方成正比,在斜面上的速度与时间成正比,故选项A错误,选项B正确。斜面长度一定时,小球从顶端滚到底端时的速度与倾角有关,从顶端滚到底端所需时间与倾角有关,故选项C、D错误。
答案:B
点拨:本题在研究小球运动时分别保持倾角一定时和斜面长度一定时。
极端法就是在解题过程中,对试题给定的已知条件进行适当的”夸大”,从而使试题原来所表示的物理现象和规律更加明显,较快地得到物理问题的正确解答的一种解题方法。求解极值问题的方法从大的角度可分为物理方法和数学方法.
物理方法包括(1)利用临界条件求极值;(2)利用问题的边界条件求极值;(3)利用矢量图求极值;
数学方法包括(1)用三角函数关系求极值;(2)用二次方程的判别式求极值;(3)用不等式的性质求极值.
特别提示:极端法只有在所研究的变量发生单调、连续变化,并存在理论极限时才适用。
例1.已知两个位置固定的点电荷之间有相互作用的斥力,它们的带电量分别为q1和q2,若将这些电量在它们之间重新分配,以使它们间的斥力最大,则它们所带的电量应分别为q1/= ,q2/= 。
解析:由库仑定律可知:F=K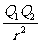 ,由于r,K均为定值,只有当Q1Q2的乘积最大时,F最大。
,由于r,K均为定值,只有当Q1Q2的乘积最大时,F最大。
只有当q/1=q2/=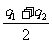 时,库仑力F最大。
时,库仑力F最大。
点评:和为定值的函数,由平均值不等式:“若a、b之和为一定值时,只有当a=b时,两者的乘积最大”
例2.(08唐山模拟)设想人类开发月球,不断把月球的矿藏搬运到地球上,假设经过长时间的开采后,地球仍可看作是均匀的球体,月球仍沿开采前的圆轨道运动,则与开采前相比( )
A.地球与月球间的万有引力将增大
B.地球与月球间的万有引力将减小
C.月球绕地球运动的周期将变长
D.月球绕地球运动的周期将变短
解析:设开始时地球的质量为M0,月球的质量为m0,月球绕地球做圆周运动的轨道半径为R.则月球与地球之间的万有引力为: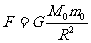 。
。
从实际出发,因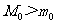 ,当月球的矿藏搬运到地球上后,地球的质量M比月球的质量m变的更大,即两个质量相差越来越大,则M与m的乘积越来越小,故地球与月球间的万有引力将减小.B选项正确.
,当月球的矿藏搬运到地球上后,地球的质量M比月球的质量m变的更大,即两个质量相差越来越大,则M与m的乘积越来越小,故地球与月球间的万有引力将减小.B选项正确.
月球绕地球运动的周期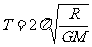 ,依题意R不变,而地球质量M越来越大,故月球绕地球运动的周期将变短.D选项正确.
,依题意R不变,而地球质量M越来越大,故月球绕地球运动的周期将变短.D选项正确.
点拨:对于两个大于零的变量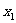 、
、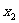 ,若其和
,若其和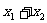 为一定值C,则当
为一定值C,则当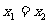 时,其积
时,其积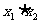 取最大值
取最大值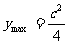 .如果
.如果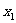 、
、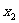 的数值相差的越大,其积
的数值相差的越大,其积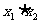 越小。
越小。
利用对称法分析解决物理问题,可以避免复杂的数学运算和推导,直接抓住问题的本质,快速简便地解决问题.利用对称法解题的思路的关键是寻找研究对象的对称性特点。
例题(2008年上海)如下左图所示,平行于y轴的导体棒以速度v向右匀速直线运动,经过半径为R、磁感应强度为B的圆形匀强磁场区域,导体棒中的感应电动势ε与导体棒位置x关系的图像是( )
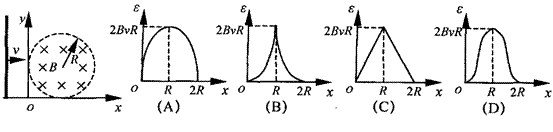 解析:在x=R左侧,设导体棒与圆的交点和圆心的连线与x轴正方向成θ角,则导体棒切割有效长度L=2Rsinθ,电动势与有效长度成正比,故在x=R左侧,电动势与x的关系为正弦图像关系,由对称性可知在x=R右侧与左侧的图像对称。答案:A
解析:在x=R左侧,设导体棒与圆的交点和圆心的连线与x轴正方向成θ角,则导体棒切割有效长度L=2Rsinθ,电动势与有效长度成正比,故在x=R左侧,电动势与x的关系为正弦图像关系,由对称性可知在x=R右侧与左侧的图像对称。答案:A
点拨:由于磁场区域是个圆面积,因此导体棒切割有效长度左右是对称的。
假设法解题是指假设一种情况成立,进一步推导,如果推出矛盾,则假设的情况不成立,如果不能推出矛盾,则假设的情况成立。在解题中这是一种“退一步”的策略,却能收到“海阔天空”的效果。
例题(07河北模拟)一根张紧的水平弹性长绳上的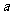 、
、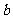 两点,相距14.0m,
两点,相距14.0m,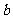 点在
点在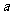 点的右方.当一列简谐横波沿此绳向右传播时,若
点的右方.当一列简谐横波沿此绳向右传播时,若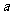 点的位移达到正极大时,
点的位移达到正极大时,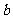 点的位移恰为零,且向下运动.经过1.00
点的位移恰为零,且向下运动.经过1.00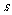 后,
后,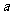 点的位移为零,且向下运动.则这列波的波速可能为
点的位移为零,且向下运动.则这列波的波速可能为
A.14m/s B.10m/s C.6m/s D.4.67m/s
解析:由题意知,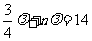 (
(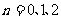 …)
…)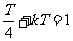 (
(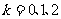 …)所以波速为
…)所以波速为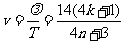 当
当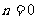
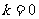 时
时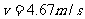 当
当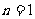
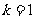 时
时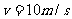 .假设
.假设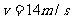 则
则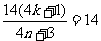 即
即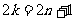 因为
因为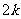 和
和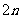 都是偶数,所以矛盾。设
都是偶数,所以矛盾。设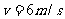 则
则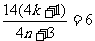 即
即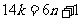 矛盾。本题答案为BD.
矛盾。本题答案为BD.
点拨:本题考察机械波的多解,由于只有四个选项,可以假设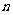 取整数、奇数、偶数来进行确定。
取整数、奇数、偶数来进行确定。
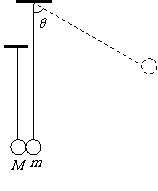 例题 (07全国理综卷Ⅰ)如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点处与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°。
例题 (07全国理综卷Ⅰ)如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点处与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场。已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处。求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°。
解析:设在第n次碰撞前绝缘球的速度为vn-1,碰撞后绝缘球、金属球的速度分别为vn、Vn。由于碰撞过程中动量守恒、碰撞前后动能相等,设速度向左,则
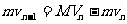
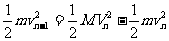
解得: 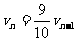
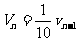
第n次碰撞后绝缘球的动能为: 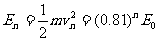
E0为第1次碰撞前的动能,即初始能量
绝缘球在θ=θ0=60°与θ=45°处的势能之比为 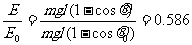
经n次碰撞后有: 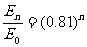
易算出(0.81)2=0656,(0.81)3=0.531,因此,经过3次碰撞后θ小于45°
点评:通过本题导出联系相邻两次作用的递推关系式,再把结论推广,后结合数学知识求解。
 等效是指不同的物理现象、模型、过程等在物理意义、作用效果或物理规律方面是相同的。它们之间可以相互替代,而保证结论不变。等效的方法是面对一个较为复杂的问题,提出一个简单的方案或设想,而使它们的效果完全相同,从而将问题化难为易,求得解决。
等效是指不同的物理现象、模型、过程等在物理意义、作用效果或物理规律方面是相同的。它们之间可以相互替代,而保证结论不变。等效的方法是面对一个较为复杂的问题,提出一个简单的方案或设想,而使它们的效果完全相同,从而将问题化难为易,求得解决。
例题如图甲,闭合线圈上方有一竖直放置的条形磁铁,磁铁的N 极朝下。当磁铁向下运动时(但未插入线圈内部),
A.线圈中感应电流的方向与图中箭头方向相同,磁铁与线圈相互吸引
B.线圈中感应电流的方向与图中箭头方向相同,磁铁与线圈相互排斥
C. 线圈中感应电流的方向与图中箭头方向相反,磁铁与线圈相互吸引
D.线圈中感应电流的方向与图中箭头方向相反,磁铁与线圈相互排斥
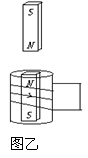 解析:当条形磁铁向下运动时,磁通量会逐渐增加,在导线中会产生感应电流,而感应电流的出现,又会使得线圈由于电磁感应而产生磁场,此时,可以将线圈等效成一个条形磁铁,如图乙所示,而这个条形磁铁对上面一个条形磁铁的作用效果应该等效与阻碍磁通量的增加,所以会对之产生排斥作用,所以可首先判断出“线圈等效条形磁铁”的极性为“上N下S”,再通过“右手定则”去判断出电流方向为图示方向。故B选项是正确的。
解析:当条形磁铁向下运动时,磁通量会逐渐增加,在导线中会产生感应电流,而感应电流的出现,又会使得线圈由于电磁感应而产生磁场,此时,可以将线圈等效成一个条形磁铁,如图乙所示,而这个条形磁铁对上面一个条形磁铁的作用效果应该等效与阻碍磁通量的增加,所以会对之产生排斥作用,所以可首先判断出“线圈等效条形磁铁”的极性为“上N下S”,再通过“右手定则”去判断出电流方向为图示方向。故B选项是正确的。
点评:此题是把线圈等效条形磁铁来确定磁铁与线圈的作用力
1. 物理模型:就是将带有实际色彩的物理对象或物理过程通过抽象、理想化、简化和类比等方法转化成理想的物理模型。原始的物理模型可分为如下两类:
物理模型:就是将带有实际色彩的物理对象或物理过程通过抽象、理想化、简化和类比等方法转化成理想的物理模型。原始的物理模型可分为如下两类:
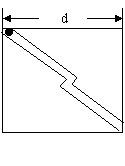
例题如图所示,宽为d、质量为M的正方形木静止在光滑水平面上,一质量m的小球由静止开始沿“Z”字通道从一端运动到另一端,求木块-和小球的对地位移。
解析:把小球和木块看成一个系统,由于水平方向所受合外力为零,则水平方向动量守恒.设小球的水平速度为v1、木块的速度为v2,则有 mv1=Mv2
若小球对地位移为 s1、木块对地位移为s2,则有 ms1=Ms2
且 s1+s2=d 解得 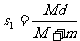
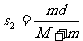
点拨:本题属于人船模型。利用人船模型及其典型变形,可使许多动量守恒问题的分析思路和解答步骤变得极为简单,有时可直接看出答案。
2.整体法适用的情况:
 (1)当只涉及研究系统而不涉及系统内部某些物体的力和运动时(2)当只涉及运动的全过程而不涉及某段运动时(3)当运用适用于系统的物理规律解题时(如动量守恒定律机械能守恒定律)可整体分析对象和整体研究过程
(1)当只涉及研究系统而不涉及系统内部某些物体的力和运动时(2)当只涉及运动的全过程而不涉及某段运动时(3)当运用适用于系统的物理规律解题时(如动量守恒定律机械能守恒定律)可整体分析对象和整体研究过程
例1(2008年海南)如图所示,质量为M的楔形物块静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.地面对楔形物块的支持力为
A.(M+m)g B.(M+m)g-F
C.(M+m)g+Fsinθ D.(M+m)g-Fsinθ
解析:本题可用整体法的牛顿第二定律解题,竖直方向由平衡条件:Fsinθ+N=mg+Mg,则N= mg+Mg-Fsinθ 。
 答案:D
答案:D
点评:本题是用取研究对象整体法,若逐个物体分析列式,求解则很复杂.应用了整体分析方法,就很容易得出结果.
例2 如图所示,金属杆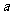 在离地
在离地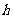 高处从静止开始沿弧形轨道下滑,导轨平行的水平部分有竖直向上的匀强磁场B,水平部分导轨上原来放有一根金属杆b,已知杆
高处从静止开始沿弧形轨道下滑,导轨平行的水平部分有竖直向上的匀强磁场B,水平部分导轨上原来放有一根金属杆b,已知杆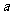 的质量为
的质量为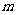 ,b杆的质量为
,b杆的质量为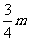 水平导轨足够长,不计摩擦,求:(1)
水平导轨足够长,不计摩擦,求:(1)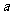 和b的最终速度分别是多大?(2)从开始到达到最终速度整个过程中回路释放的电能是多少?
和b的最终速度分别是多大?(2)从开始到达到最终速度整个过程中回路释放的电能是多少?
解析:(1)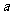 下滑
下滑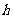 过程中机械能守恒:
过程中机械能守恒: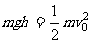 ①
①
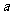 进入磁场后,回路中产生感应电流,
进入磁场后,回路中产生感应电流,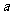 、b都受安培力作用,
、b都受安培力作用,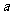 作减速运动,b作加速运动,经一段时间,
作减速运动,b作加速运动,经一段时间,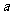 、b速度达到相同,之后回路的磁通量不发生变化,感应电流为零,安培力为零,二者匀速运动,匀速运动的速度即为
、b速度达到相同,之后回路的磁通量不发生变化,感应电流为零,安培力为零,二者匀速运动,匀速运动的速度即为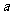 、b的最终速度,设为
、b的最终速度,设为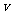 ,由过程中
,由过程中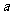 、b系统所受合外力为零,动量守恒得:
、b系统所受合外力为零,动量守恒得: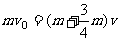 ② 由①②解得最终速度
② 由①②解得最终速度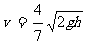 .
.
(2)由能量守恒知,回路中产生的电能等于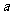 、b系统机械能的损失,所以,
、b系统机械能的损失,所以,
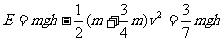 .
.
点评:本题运用了研究对象和研究过程整体法,并以两杆整体的受力及全过程运动和能量为主要线索列方程求解。
1.“整体法”的含义:
在研究一个复杂现象(复杂过程)时,若这些复杂现象(复杂过程)的中间过程或中间环节对整个现象没影响,则可对整个过程或整个系统进行整体研究,此种研究方法称为“整体法”。
2.隔离法的适用情况:(1)求解某段运动中物体的运动规律;(2).求解物体间的相互作用;
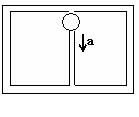 例题如图所示,质量为M的木箱放在水平面上,木箱中的立杆上套着一个质量为m的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的1/2,即a=
例题如图所示,质量为M的木箱放在水平面上,木箱中的立杆上套着一个质量为m的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的1/2,即a=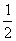 g,则小球在下滑的过程中,木箱对地面的压力为多少?
g,则小球在下滑的过程中,木箱对地面的压力为多少?
解析:木箱对地面的压力决定于木箱的重力及立杆受到小球的作用力。木箱静止,小球加速下滑,二者没有共同的加速度,用“整体法”列方程解题对大多数同学则难以理解,如把小球隔离出来,以小球为研究对象,由牛顿第二定律列方程则易于理解。
以小球m为研究对象,受重力mg及摩擦力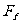 ,由牛顿第二定律得:mg-
,由牛顿第二定律得:mg-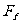 =ma,以木箱M为研究对象,受重力Mg地面支持力
=ma,以木箱M为研究对象,受重力Mg地面支持力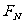 及小球给予的摩擦力
及小球给予的摩擦力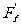 ,木箱处于平衡状态,则有:
,木箱处于平衡状态,则有: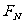 -
-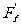 -Mg=0,由牛顿第三定律得:
-Mg=0,由牛顿第三定律得: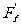 =
=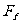 ,由上述三式可得:
,由上述三式可得: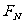 =
=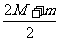 g,由牛顿第三定律可知:木箱对地面的压力大小为
g,由牛顿第三定律可知:木箱对地面的压力大小为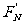 =
=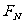 =
=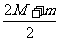 g
g
点评:本题是隔离加速度不同的木箱和小球,然后根据牛顿定律列方程求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com