
5.理解万有引力定律
(1)万有引力定律: 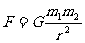 ,G=6.67×10-11N.m2/kg2.适用条件:适用于相距很远,可以看做质点的两物体间的相互作用,质量分布均匀的球体也可用此公式计算,其中r指球心间的距离。
,G=6.67×10-11N.m2/kg2.适用条件:适用于相距很远,可以看做质点的两物体间的相互作用,质量分布均匀的球体也可用此公式计算,其中r指球心间的距离。
(2)万有引力定律的应用
①万有引力近似等于重力: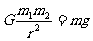
讨论重力加速度g随离地面高度h的变化情况: 物体的重力近似为地球对物体的引力,即mg=G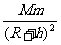 。所以重力加速度g= G
。所以重力加速度g= G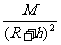 ,可见,g随h的增大而减小。
,可见,g随h的增大而减小。
②万有引力提供向心力: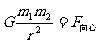
求天体的质量:通过观天体卫星运动的周期T和轨道半径r或天体表面的重力加速度g和天体的半径R,就可以求出天体的质量M。3求解卫星的有关问题:根据万有引力等于卫星做圆周运动的向心力可求卫星的速度、周期、动能、动量等状态量。由G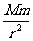 =m
=m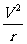 得V=
得V=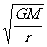 ,由G
,由G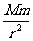 = mr(2π/T)2得T=2π
= mr(2π/T)2得T=2π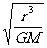 。由G
。由G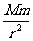 = mrω2得ω=
= mrω2得ω=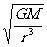 ,由Ek=
,由Ek=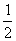 mv2=
mv2=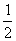 G
G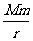 。
。
4.理解圆周运动的规律
(1)两种模型:凡是直接用皮带传动(包括链条传动、摩擦传动)的两个轮子,两轮边缘上各点的线速度大小相等;凡是同一个轮轴上(各个轮都绕同一根轴同步转动)的各点角速度相等(轴上的点除外)。
(2) 描述匀速圆周运动的各物理量间的关系: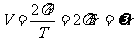
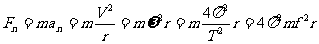 .
.
(3)竖直面内圆周运动最高点处的受力特点及分类:
①弹力只可能向下,如绳拉球。②弹力只可能向上,特例如车过桥。③弹力既可能向上又可能向下,如管内转球(或杆连球、环穿珠)。弹力可取任意值。但可以进一步讨论:当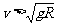 时物体受到的弹力必然是向下的;当
时物体受到的弹力必然是向下的;当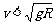 时物体受到的弹力必然是向上的;当
时物体受到的弹力必然是向上的;当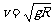 时物体受到的弹力恰好为零。当弹力大小F<mg时,向心力有两解:mg±F;当弹力大小F>mg时,向心力只有一解:F +mg;当弹力F=mg时,向心力等于零。
时物体受到的弹力恰好为零。当弹力大小F<mg时,向心力有两解:mg±F;当弹力大小F>mg时,向心力只有一解:F +mg;当弹力F=mg时,向心力等于零。
3.理解平抛物体的运动的处理方法
(1)平抛运动的处理方法:把平抛运动看作为两个分运动的合动动:一个是水平方向(垂直于恒力方向)的匀速直线运动,一个是竖直方向(沿着恒力方向)的匀加速直线运动。
(2)平抛运动的性质:做平抛运动的物体仅受重力的作用,故平抛运动是匀变速曲线运动。
(3)临界问题: 典型例题很多,如:在排球运动中,为了使从某一位置和某一高度水平扣出的球既不触网、又不出界,扣球速度的取值范围应是多少?
2、理解运动的合成与分解
(1)运动的合成与分解的四性:分运动的独立性;运动的等效性(合运动和分运动是等效替代关系,不能并存);运动的等时性;运动的矢量性(加速度、速度、位移都是矢量,其合成和分解遵循平行四边形定则。)
(2)连带运动问题:指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相同求解。
1、理解曲线运动的条件
运动物体所受合外力的方向跟其速度方向不在一条直线上时,物体做曲线运动。
17.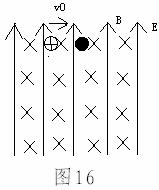 如图16所示,在足够大的空间内,同时存在着竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=1.57T,小球1带正电,其电荷量与质量之比
如图16所示,在足够大的空间内,同时存在着竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=1.57T,小球1带正电,其电荷量与质量之比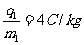 ,所受重力与电场力的大小相等,小球2不带电,静止放置于固定的水平悬空支架上,小球1向右以
,所受重力与电场力的大小相等,小球2不带电,静止放置于固定的水平悬空支架上,小球1向右以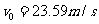 的水平速度与小球2正碰,碰后经过0.75s再次相碰。设碰撞前后两小球带电情况不发生改变,且始终在同一竖直平面内。(g=10
的水平速度与小球2正碰,碰后经过0.75s再次相碰。设碰撞前后两小球带电情况不发生改变,且始终在同一竖直平面内。(g=10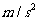 )问
)问
(1) 电场强度E的大小是多少?
(2)
两小球的质量之比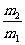 是多少?
是多少?
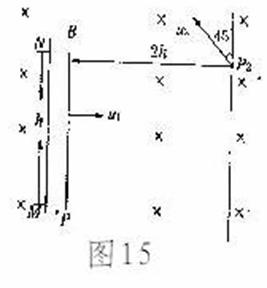
16. 设在讨论的空间范围内有磁感应强度为B的匀强磁场,B的方向垂直于纸面向里,如图15所示,在纸平面上有一长为h的光滑绝缘空心细管MN,管的M端内有一带正电的小球P1,在纸平面上N端的正右前方2h处有一个不带电的小球P2,开始时P1相对管静止,管向运动,小球P2在纸平面上沿着以于MN延长线方向成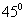 角的速度
角的速度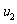 运动,设管的质量远大于P1的质量,P1在管内的运动对管的运动的影响可以忽略。
运动,设管的质量远大于P1的质量,P1在管内的运动对管的运动的影响可以忽略。
已知P1离开的管的N端时相对纸面的速度大小恰好为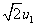 ,且在离开管后最终能与P2相碰,试求:(1)P1的比荷
,且在离开管后最终能与P2相碰,试求:(1)P1的比荷
(2)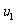 和
和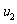 的比值
的比值
15.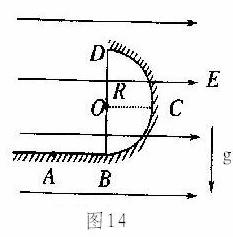 如图14所示,ABCD表示竖立在场强为
如图14所示,ABCD表示竖立在场强为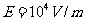 的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与半圆环相切,A为水平轨道上的一点,而且,AB=R=0.2m,把一质量m=10g、带电量q=
的水平匀强电场中的绝缘光滑轨道,其中轨道的BCD部分是半径为R的半圆环,轨道的水平部分与半圆环相切,A为水平轨道上的一点,而且,AB=R=0.2m,把一质量m=10g、带电量q=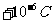 的小球在水平轨道的A点由静止释放后,小球在轨道的内侧运动(g=10
的小球在水平轨道的A点由静止释放后,小球在轨道的内侧运动(g=10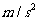 )。求:
)。求:
(1)小球到达C点时的速度
(2)小球达到C点时对轨道的压力
(3)要使小球刚好能运动到D点,小球开始运动的位置应离B点多远?
14.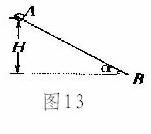 如图13所示,质量为m的小球A在绝缘细杆上,杆的倾角为
如图13所示,质量为m的小球A在绝缘细杆上,杆的倾角为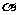 ,小球A带正电,电量为q。在杆上B点处固定一个电量为Q的正电荷,将小球A由距B点竖直高度为H处无初速度释放,小球A下滑过程中电量不变,不计A与细杆间的摩擦,整个装置处在真空中,已知静电力常量k和重力加速度g
,小球A带正电,电量为q。在杆上B点处固定一个电量为Q的正电荷,将小球A由距B点竖直高度为H处无初速度释放,小球A下滑过程中电量不变,不计A与细杆间的摩擦,整个装置处在真空中,已知静电力常量k和重力加速度g
(1)A球刚释放时的加速度是多大?
(2)当A球的动能最大时,球此时A球与B点的距离
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com