
2.D.[解析]由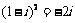 ,故选D.
,故选D.
[链接高考]高考对复数部分的考查要求较低,通常以送分题形式给出,本题是对运用复数的简单运算及复数的几何意义的考查.
1.B.[解析]由题意知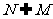 ,所以
,所以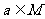 不一定能得到
不一定能得到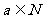 ,但
,但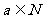 一定得到
一定得到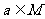 ,由此得到答案B.
,由此得到答案B.
[链接高考]集合是高中数学的基本概念之一,它与不等式、充要条件或其他任何知识联系起来,属于容易题.
21.(本小题满分14分)
设函数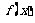 的定义域为R,当x<0时,
的定义域为R,当x<0时,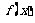 >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有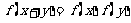 .
.
(1)求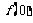 ,判断并证明函数
,判断并证明函数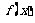 的单调性;
的单调性;
(2)数列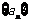 满足
满足 ,且
,且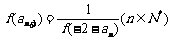 ,
,
①求 通项公式;
通项公式;
②当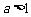 时,不等式
时,不等式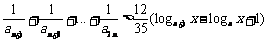 对不小于2的正整数
对不小于2的正整数
恒成立,求x的取值范围.
[答案及详细解析]
20.(本小题满分14分)
已知椭圆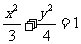 的焦点F与抛物线C:
的焦点F与抛物线C: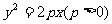 的焦点关于直线x-y=0
的焦点关于直线x-y=0
对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab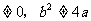 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,
BM与抛物线的另一交点为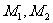 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要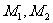 存在
存在
且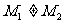 )直线
)直线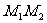 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.
19.(本小题满分14分)
已知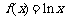 ,
,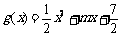 (
(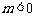 ),直线
),直线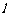 与函数
与函数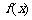 、
、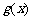 的图像都相切,且与函数
的图像都相切,且与函数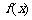 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(1)求直线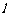 的方程及
的方程及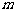 的值;
的值;
(2)若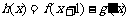 (其中
(其中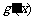 是
是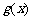 的导函数),求函数
的导函数),求函数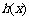 的最大值;
的最大值;
(3)当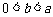 时,比较
时,比较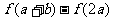 与
与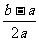 .
.
18.(本小题满分14分)
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,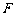 为
为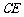 上的点,且BF
上的点,且BF
⊥平面ACE.
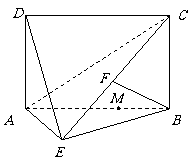 (1)求证:AE⊥BE;
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试
在线段CE上确定一点N,使得MN∥平面DAE.
17.(本小题满分12分)
已知集合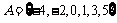 ,在平面直角坐标系中,点
,在平面直角坐标系中,点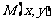 的坐标x∈A,y∈A.计算:
的坐标x∈A,y∈A.计算:
(1)点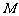 正好在第二象限的概率;
正好在第二象限的概率;
(2)点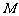 不在x轴上的概率;
不在x轴上的概率;
(3)点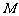 正好落在区域
正好落在区域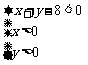 上的概率.
上的概率.
16.(本小题满分12分)
已知x是三角形的内角,且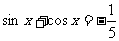 .
.
(Ⅰ)求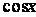 的值;
的值;
(Ⅱ)求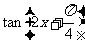 的值.
的值.
(二)选做题(14-15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在极坐标系中,点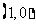 到直线
到直线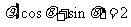 的距
的距
离为 .
15.(几何证明选讲选做题)如图2所示,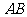 与
与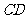 是⊙O
是⊙O
的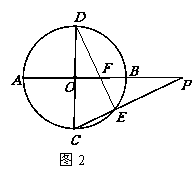 直径,
直径,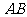
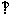
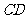 ,
,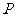 是
是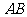 延长线上一点,连
延长线上一点,连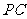 交
交
⊙O于点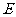 ,连
,连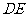 交
交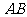 于点
于点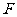 ,若
,若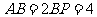 ,
,
则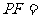 .
.
(一)必做题(11-13题)
11.某中学号召学生在暑假期间至少参加一次社会公益活动(以下简
称活动).该校文学社共有100名学生,他们参加活动的次数统计如
图所示.则从文学社中任意选1名学生,他参加活动次数为3的概率
是 、该文学社学生参加活动的人均次数为 .
12.用二分法求方程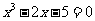 在区间
在区间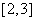 上的近似解,取区间中点
上的近似解,取区间中点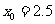 ,那么下一个有解区间为 .
,那么下一个有解区间为 .
13.设函数 上的奇函数,且满足
上的奇函数,且满足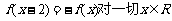 都成立,又
都成立,又
当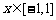 时,
时,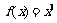 ,则下列四个命题:
,则下列四个命题:
①函数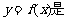 以4为周期的周期函数; ②当
以4为周期的周期函数; ②当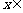 [1,3]时,
[1,3]时,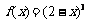 ;
;
③函数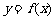 的图象关于
的图象关于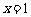 对称; ④函数
对称; ④函数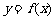 的图象关于点(2,0)对称.
的图象关于点(2,0)对称.
其中正确的命题序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com