
1、. 电脑”扫雷”游戏的操作面被平均分成480块,其中有99块埋有地雷,现在操作面上任意点击一下,碰到地雷的概率为( )
A.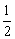 B.
B.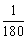 C.
C.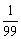 D.
D.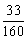
2、复习两个互斥事件的概率加法公式并能综合应用.
[课堂互动]
自学评价
1、复习几何概型的概率公式并能综合应用;
3、从一副52张(不含大小王)扑克牌中抽出一张,放回后重新洗牌,再抽出一张,
(1)前后两张为同花色的概率是多少?
(2)是同一张的概率是多少?
2、一辆班车接送职工上下班,规定有10个车站,车上有30人,如果某站无人下车,则班车在此站不停,求下列事件的概率.
(1)班车在某一站停车的概率;
(2)班车停车不少于2次的概率.
1、下列说法中正确的是( )
A.事件A、B中至少有一个发生的概率一定比A、B中恰有一个发生的概率大
B.事件A、B同时发生的概率一定比事件A、B恰有一个发生的概率小
C.互斥事件一定是对立事件,对立事件不一定是互斥事件
D.互斥事件不一定是对立事件,对立事件一定是互斥事件
2、互斥事件与对立事件的区别与联系:互斥事件是指事件A与事件B在一次试验中不会同时发生,其具体包括三种不同的情形:(1)事件A发生且事件B不发生;(2)事件A不发生且事件B发生;(3)事件A与事件B同时不发生,而对立事件是指事件A 与事件B有且仅有一个发生,其包括两种情形;(1)事件A发生B不发生;(2)事件B发生事件A不发生,对立事件是互斥事件的特殊情形.
[经典范例]
例1 抛掷一骰子,观察掷出的点数,设事件A为“出现奇数点”,B为“出现偶数点”,已知P(A)=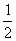 ,P(B)=
,P(B)=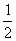 ,求 “出现奇数点或偶数点”的概率.
,求 “出现奇数点或偶数点”的概率.
[分析]抛掷骰子,事件“出现奇数点”和“出现偶数点”是彼此互斥的,可用运用概率的加法公式求解.
[解]
例2 盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
[解]
例3 如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是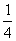 ,取到方块(事件B)的概率是
,取到方块(事件B)的概率是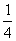 ,问:
,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
[分析]事件C是事件A与事件B的并,且A与B互斥,因此可用互斥事件的概率和公式求解,事件C与事件D是对立事件,因此P(D)=1-P(C).
[解]
例4 袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为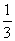 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是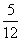 ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是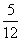 ,试求得到黑球、得到黄球、得到绿球的概率各是多少?
,试求得到黑球、得到黄球、得到绿球的概率各是多少?
[分析]利用方程的思想及互斥事件、对立事件的概率公式求解.
[解]
追踪训练
1、在一个盒子内放有10个大小相同的小球,其中有7个红球、2个绿球、一个黄球.现从中摸出1个球:
事件A:“从盒中摸出1个球,得到红球”;
事件B:“从盒中摸出1个球,得到绿球”;
事件C:“从盒中摸出1个球,得到黄球”,
上述事件中,哪些是互斥事件?
答:不能同时发生的两个事件叫做互斥事件.上述事件中,事件A和B、B和C、A和C是互斥事件.
2、提高两个互斥事件的概率加法公式的综合应用能力。
[课堂互动]
自学评价
1、进一步巩固两个互斥事件的概率加法公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com