2.2 高能磷酸化合物水解释能的例证

要弄清楚ATP水解是否释放能量，可以从三磷酸的水解入手，因为三磷酸的水解与ATP的水解在旧化学键的断裂和新化学键的形成具有很大的相似性。同理，ADP的水解可以焦磷酸的水解进行类比(图2)。

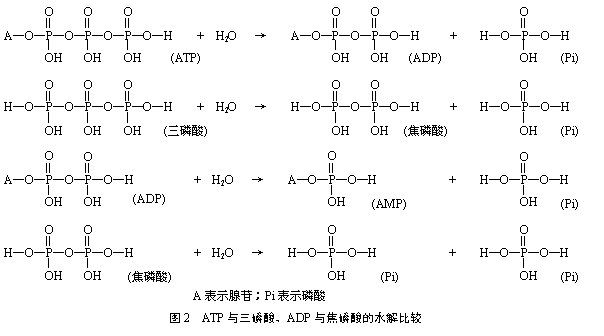
正磷酸在强热条件下发生脱水作用，依次生成焦磷酸(H₄P₂O₇)、三磷酸(H₅P₃O₁₀)和偏磷酸[(HPO₃)_n](图3)。根据反应条件可以推测，这些反应均应为吸热反应，且生成三磷酸需要吸收更多的能量。

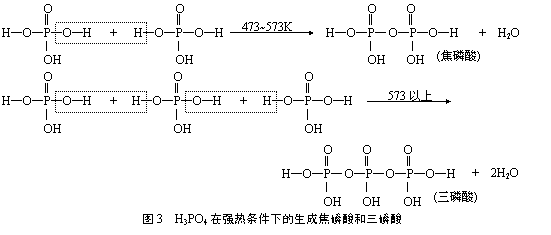
焦磷酸、三磷酸和偏磷酸均易溶于水，且在溶液中水解逐渐转变为正磷酸。根据部分物质的标准摩尔生成焓(表1)可以进行焦磷酸水解生成正磷酸的反应热计算，得到 “H₄P₂O₇(l)+H₂O(l) =2H₃PO₄(l)；△_rH_m^y= -25.9kJ•mol^-1”。由此可知，焦磷酸水解放热且放出的高达25.9 kJ•mol^-1>20.92kJ•mol^-1(高能磷酸化合物的判据)，因此焦磷酸也属于高能磷酸化合物。

表1 几种物质的标准摩尔生成焓(单位：kJ•mol^-1)

焦磷酸的水解类似ADP的水解，因此生物教材中也认为ADP中存在1个“高能磷酸键”。三磷酸水解应该释放出比焦磷酸水解更多的能量，这与ATP水解释放比ADP水解更多的能量是相符的。因此，ATP或ADP的能量来源是水解释能，而非“高能磷酸键”断键释能，P-O键的断裂只是水解的方式。

2.1 高能磷酸化合物中有没有高能磷酸键

根据ATP的结构(图1)可知，ATP实际上就是由腺嘌呤、核糖与3分子磷酸缩合而成的游离核苷酸，磷酸与磷酸间以磷酸酐键相连，ATP水解时(磷酸酐键断裂)释放的能量高达30.54 kJ•mol^-1，而一般的磷酸酯水解时(磷酸酯键断裂)释放的能量只有8~12kJ•mol^-1。高能磷酸化合物是指水解时释放的能量在20.92 kJ•mol^-1以上的磷酸化合物，显然ATP也是高能磷酸化合物。生物学上同时也将这种磷酸酐键称为“高能磷酸键”，这样的名称是不够确切的。

首先，一种化合物水解时释放能量的多少取决于该化合物整个分子的结构，以及反应物能量与产物能量的差异，而不是由哪个特殊化学键的破坏所致。其次，无论简单磷酸盐或复杂磷酸盐的基本结构单元是磷氧四面体，即这些P-O键之间并无本质区别，因此也不可能存在所谓的“高能磷酸键”。第三，从高能磷酸化合物的定义可以看出，高能磷酸化合物是以每摩尔化合物水解释放的能量多少来判断的，而不是根据是否存在“高能磷酸键”来定义的，可见，“高能磷酸键”也是子虚乌有。但为了叙述及解释问题方便，高能磷酸键的概念至今仍被生物界采用。

1.2 “化学键储能”违背了物质与能量的基本关系

“高能磷酸键断裂释能”的认识基础是“高能磷酸键中储存着很高的能量”，即“化学键中储存着能量”，这与物质与能量的基本关系--“物质之中蕴含能量”是矛盾的。若以“化学键中储存着能量”来分析“H-H→••H+•H”这一过程，则同样可以得出这样一个结论“物质中蕴含的能量是降低的”，即1个H₂分子的能量比2个H原子的能量高，这与事实也是不相符的。

2 对“高能磷酸键水解释能”的评析

1.1 “断键释能”违背了化学键的一般认识

在高中化学甚至大学化学中，认为化学反应过程实质上就是旧的化学键断裂、新的化学键形成的过程，且化学键断裂需要吸收能量，化学键形成则会放出能量。同时，还通俗地将“打断1摩尔化学键所需要的能量”^[2]定义为键能。倘若以“化学键断裂释能”来分析“H-H→••H+•H”这一过程，则有“△H<0，△S>0”，就可以得出一个可怕的结论“恒温恒压条件下H-H→••H+•H一定能自发进行”。

11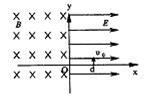．如图所示，在x>0的空间中，存在沿x轴方向的匀强电场，电场强度正E=10　 N／C；　 在x<O的空间中，存在垂直xoy平面方向的匀强磁场，磁感应强度B=0.5T．一带负 电的粒子(比荷q／m=160C／kg)，在x=0.06m处的d点以v₀=8m／s的初速度沿y轴正方向开始运动，不计带电粒子的重力，求：

　　 (1)带电粒子开始运动后第一次通过y轴时距O点的距离．

　　 (2)带电粒子进入磁场后经多长时间返回电场．

　　 (3)带电粒子运动的周期．

　 解：(1)对于粒子在电场中的运动：　

　 第-次通过y轴的交点到O点的距离为y_l=v₀t　　

　 将数据代入解得　　 y₁=0.069(m)　

　 (2)x方向的速度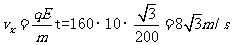

　设进入磁场时速度与y轴的方向为，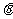

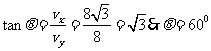
所以在磁场中作圆周运动所对应的圆心角为　 带电粒子在磁场中做匀速圆周运动周期为 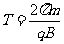　　带电粒子在磁场中运动的时间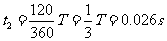

从开始至第一次到达y轴的时间

从磁场再次回到电场中的过程(未进入第二周期)是第一次离开电场时的逆运动

根据对称性，t₃=t₁　 因此粒子的运动周期为

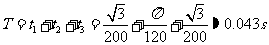
10、(1)带电粒子从C孔进入，与筒壁碰撞2次再从C孔射出经历的时间为最短．

由　　　 qE＝mv²　 ……………………………………… 2分

粒子由C孔进入磁场，在磁场中做匀速圆周运动的速率为

v＝……………………………………………1分

由　　 r＝　　 即Rcot30°＝　 ………………………………3分

得　　 B＝　 ……………………………………2分

(2)粒子从A→C的加速度为

a＝qE／md　 …………………………………………2分

由 d＝at₁²／2，粒子从A→C的时间为

　　　　　　 t₁＝=d ………………………………… 2分

粒子在磁场中运动的时间为

　　　　　　　 t₂＝T／2＝πm／qB ………………………………… 2分

将(1)求得的B值代入，

得　　　　 t₂＝πR ……………………………………… 1分

求得　　　 t＝2t₁+t₂＝(2d +πR)………………………1分

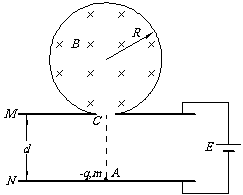
10．如图所示，在半径为R的绝缘圆筒内有匀强磁场，方向垂直纸面向里，圆筒正下方有小孔C与平行金属板M、N相通。两板间距离为d，两板与电动势为E的电源连接，一带电量为－q、质量为m的带电粒子(重力忽略不计)，开始时静止于C点正下方紧靠N板的A点，经电场加速后从C点进入磁场，并以最短的时间从C点射出。已知带电粒子与筒壁的碰撞无电荷量的损失，且碰撞后以原速率返回。求：

⑴筒内磁场的磁感应强度大小；

⑵带电粒子从A点出发至重新回到A点射出所经历的时间。

9．解：带电粒子进入电场，经电场加速。

根据动能定理：　　　 q U＝mv²/2　　

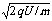所以　　　　 v＝　　　 (3分)

粒子进入磁场后做匀速圆周运动，轨迹如图。

设圆周半径为R　，在三角形ode中 ，有

　　　 (L－R)²+(L/2)²=R² (3分)

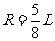　　　　　　　　　 (2分)

又　　　　　　　 q v B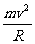＝　　　　　　　 (2分)

　　 联立求解，得

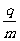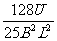=　　　　　　　　　　　　　　 (5分)

9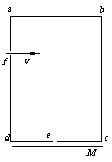．在研究性学习中，某同学设计了一个测定带电粒子比荷的实验，其实验装置如图所示。abcd是一个长方形盒子，在ad边和cd边上各开有小孔f和e，e是cd边上的中点，荧光屏M贴着cd放置，能显示从e孔射出的粒子落点位置。盒子内有一方向垂直于abcd平面的匀强磁场，磁感应强度大小为B。粒子源不断地发射相同的带电粒子，粒子的初速度可忽略。粒子经过电压为U的电场加速后，从f孔垂直于ad边射入盒内。粒子经磁场偏转后恰好从e孔射出。若已知fd=cd=L，不计粒子的重力和粒子之间的相互作用力。请你根据上述条件求出带电粒子的比荷q/m。

8.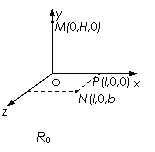如图所示，oxyz坐标系的y轴竖直向上，在坐标系所在的空间存在匀强电场和匀强磁场，电场方向与x轴平行．从y轴上的M点(0，H，0)无初速释放一个质量为m、电荷量为q的带负电的小球，它落在xz平面上的N(l，0，b)点(l>0，b>0)．若撤去磁场则小球落在xz平面的P点(l，0，0)．已知重力加速度为g．

(1)已知匀强磁场方向与某个坐标轴平行，试判断其可能的具体方向．

(2)求电场强度E的大小．

(3)求小球落至N点时的速率v．

(1)用左手定则判断出：磁场方向为－x方向或－y方向．

(2)在未加匀强磁场时，带电小球在电场力和重力作用下落到P点，设运动时间为t，小球自由下落，有　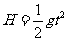　　　　　　　　　　　　　　　　　 ①

小球沿x轴方向只受电场力作用　　 　　　　　　　　　　　　　②

小球沿x轴的位移为　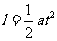　　　　　　　　　　　　　　　　　 ③

小球沿x轴方向的加速度　　　　　　　　　　　　　　　　　 ④

联立求解，得　　　　　　　　　　　　　　　　　　　　 ⑤

(3)带电小球在匀强磁场和匀强电场共存的区域运动时，洛仑兹力不做功

电场力做功为　　　　W_E=qEl　　　　　　　　　　　　　　 　　　⑥

重力做功为　　　　　W_G=mgH　　　　　　　　　　　　　　　　 ⑦

设落到N点速度大小为v,根据动能定理有

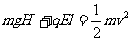　　　　　　　　　　　　　 ⑧

解得　　　　　　　　　　　　　　　　　　　 ⑨