
(一)必做题(9-12题)
9.2.解析:因为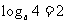 ,则
,则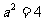 ,而
,而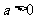 ,所以
,所以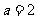 .
.
10.6.解析:由杨辉三角或二项展开式即得结论.
11.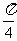 .解析:由正弦定理得:
.解析:由正弦定理得: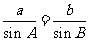 ,而
,而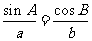 ,两式相乘得
,两式相乘得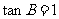 ,从而
,从而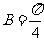 .
.
12.  .解析:依题意得
.解析:依题意得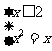 ,或
,或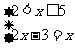 ,或
,或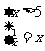 ,解得
,解得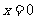 ,或
,或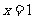 ,
,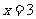 .
.
8. D. 解析: 由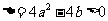 ,即
,即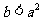 ,再通过画图,利用积分求出合乎条件的区域面积为
,再通过画图,利用积分求出合乎条件的区域面积为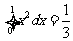 ,而所有可能的区域面积为1,由几何概型的概率为其面积的比值即可得出.
,而所有可能的区域面积为1,由几何概型的概率为其面积的比值即可得出.
7.C. 解析:仅②③正确,③是“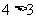 或
或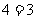 ”; ④
”; ④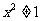 的充要条件是
的充要条件是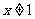 且
且 .
.
6. A. 解析: 由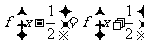 得:
得: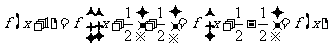 ,即1是
,即1是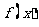 的周期,而
的周期,而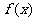 为奇函数,则
为奇函数,则
5.B. 解析:可行域三角形的三个顶点坐标为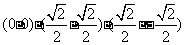 , 将这三点代入即可求得
, 将这三点代入即可求得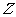 的最小值.
的最小值.
4.C. 解析: 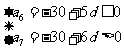 ,解得
,解得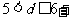
3. B. 解析:几何体为圆锥,母线长为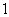 ,底面半径为
,底面半径为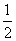 ,则侧面积为
,则侧面积为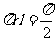 .
.
2.A. 解析:由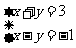 ,解得
,解得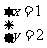 ,所以
,所以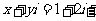 对应的点在第一象限.
对应的点在第一象限.
1. D.解析:画数轴即可.
21.(本小题满分14分)
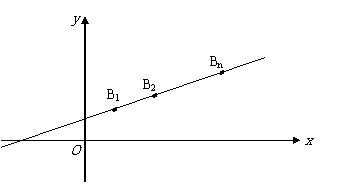
已知点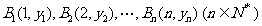 在直线
在直线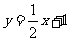 上,点
上,点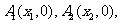
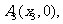 ……,
……,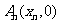 顺次为
顺次为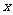 轴上的点,其中
轴上的点,其中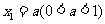 ,对于任意
,对于任意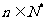 ,
,
点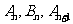 构成以
构成以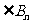 为顶角的等腰三角形, 设
为顶角的等腰三角形, 设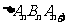 的面积为
的面积为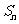 .
.
(1)
证明:数列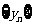 是等差数列;
是等差数列;
(2)
求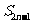 (用
(用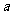 和
和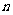 的代数式表示);
的代数式表示);
(3)
 设数列
设数列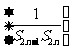 前
前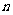 项和为
项和为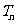 ,判断
,判断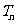 与
与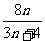 (
(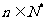 )的大小,并证明你的结论.
)的大小,并证明你的结论.
[答案及详细解析]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com