
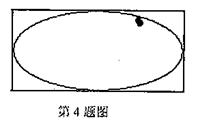
4.如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,
数得落在椭圆外的黄豆数为96颗,以此实验数据为依据
可以估计出椭圆的面积约为 ( )
A.7.68 B.16.32
C.17.32 D.8.68
3.设命题p: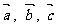 是三个非零向量;命题q:
是三个非零向量;命题q: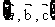 为空间的一组基向量,则命题p是命题q的 ( )
为空间的一组基向量,则命题p是命题q的 ( )
A.充分不必要条件 B.必要不充分条件
 C.充要条件 D.既非充分又非必要条件
C.充要条件 D.既非充分又非必要条件
2.有4个命题:(1)没有男生爱踢足球;(2)所有男生都不爱踢足球;(3)至少有一个男生不爱踢足球;(4)所有女生都爱踢足球;其中是命题“所有男生都爱踢足球”的否定是 ( )
A.(1) B.(2) C.(3) D.(4)
1.已知集合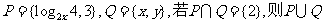 等于 ( )
等于 ( )
A.{2,3} B.{1,2,3}
C.{1,-1,2,3} D.{2,3,x,y}
22. (本题满分14分)
(本题满分14分)
已知函数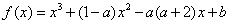
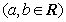 。
。
(Ⅰ)若函数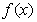 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是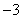 ,求
,求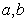 的值;
的值;
(Ⅱ)若函数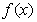 在区间
在区间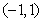 上不单调,求
上不单调,求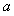 的取值范围。
的取值范围。
答案1-6 D D A B D D 7-12 B D B B A B

20.(本小题满分12分)
设数列{an}的前n项和为Sn,已知a1=1且满足3Sn2=an(3Sn-1),n≥2。
(Ⅰ)求证:{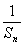 }是等差数列;
}是等差数列;
(Ⅱ)设bn=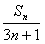 ,数列{bn}的前项和为Tn,,求T。
,数列{bn}的前项和为Tn,,求T。
21(本题满分12分)
已知在正项数列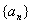 中,
中,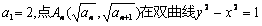 ,
,
数列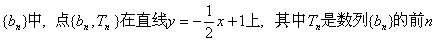 项和。
项和。
(Ⅰ)求数列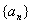 、
、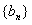 的通项公式;
的通项公式;
(Ⅱ)若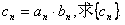 的前n项和
的前n项和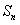 。
。
19.(本小题满分12分)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。
(Ⅰ)求只赛3局结束这次比赛的概率;
(Ⅱ)求赛4局结束这次比赛,且甲获得这次比赛胜利的概率。
18.(本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且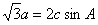 。
。
(Ⅰ)确定角C的大小:
(Ⅱ)若c=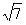 ,且△ABC的面积为
,且△ABC的面积为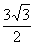
 ,求a+b的值。
,求a+b的值。
17.(本小题满分12分)
设函数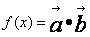 .其中向量
.其中向量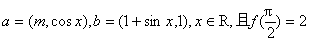 。
。
(Ⅰ)求实数没m的值;
(Ⅱ)求函数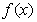 的最小值。
的最小值。
16.在区间[0,2]上随机取一个数x,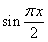 的值介于0到
的值介于0到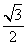 之间的概率为_______________。
之间的概率为_______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com