
|
|||
|
|||
有些老师常在序言课上板着面孔提出要“认真听讲,认真做好作业,课前要预习,课后要复习”的要求,这些自学生跨进校门之日起就听惯了的老调,并没有多少效果。我们的做法是让学生自由讨论,各抒己见。因为通过以上活动,学生对立体几何的兴趣被点燃以后,便自然想到:“我们怎样才能学好立几知识呢?经过讨论以后,教师再归纳得出学好立几的主要方法:①加强与平几知识的联系,注意用对比的方法区别异同,掌握实质;②注意对实物、教具和模型的观察和分析,培养空间想象能力;③自己动手制作模型,以加深对立几知识的理解和应用。为了学好第一章,我们要求学生准备好硬纸板三块(代平面用),竹针或铅丝四根(代直线用),在学习中随时进行模型演示,以逐步建立起空间观念。
部分学生认为立体几何比平面几何难学,存在畏惧心理;多数学生对能不能学好这门功课信心不足,对怎样学习这门功课心中无数。这种消极心理状态必然会给学习造成消极影响。因此在序言课教学中,应把排除上述心理障碍,激发学生学习立体几何的兴趣作为首先任务。
1.尽量引用实例。
“引言”中指出,“建造厂房、制造机器、修筑堤坝等,都需要进一步研究空间图形的问题。”为了使学生真正认识到立体几何是一门应用广泛的基础学科,我们在序言课上展示学校教学楼的建筑图纸,学生争相观看,兴趣盎然,并能辨认出:“这就是我们的教学楼!”教者由此指出:“没有立体几何知识,这张图纸是画不出来的。”“同学们能从图纸上看出是我们的教学楼,这说明大家已具有一定的空间想象能力,这正是学习立体几何的基础。有这样好的基础,何愁学不好它?”听到这些鼓励,学生常露出自信的微笑。
立体几何序言课以课本中的“引言”为主要教学内容,让学生对立体几何这门功课有一个粗略的整体性了解,在学习具体内容之前有一个积极的思想准备。通过序言课的教学,学生明白了立体几何研究的内容及学习立体几何的目的,就能为以后的学习打下一个良好的基础。
然而有的老师对序言课却不够重视,把已经十分抽象概括的“引言”进一步抽象概括,开课后草草几句便开始了“平面”的教学。教师急急匆匆,学生稀里糊涂,极易给后继学习带来消极影响。
由此可见,教师在充分认识序言课重要性的前提下,认真组织教学,努力完成序言课的教学任务,对提高立体几何课的教学效益是至关重要的。
27、(山西05)在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区。
(1)求圆形区域的面积(π取3.14);
(2)某时刻海面上出现一渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离(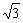 ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);
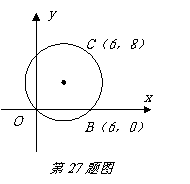 (3)当渔船A由(2)中位置向正西方航行时,是否会进入海洋生物保护区?通过计算回答。
(3)当渔船A由(2)中位置向正西方航行时,是否会进入海洋生物保护区?通过计算回答。
(08资阳)如图8,小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
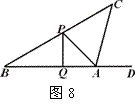 (2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC约为多少?(结果可保留根号)
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC约为多少?(结果可保留根号)
26、(08泸州)如图,在气象站台A的正西方向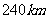 的B处有一台风中心,该台风中心以每小时
的B处有一台风中心,该台风中心以每小时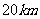 的速度沿北偏东
的速度沿北偏东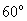 的BD方向移动,在距离台风中心
的BD方向移动,在距离台风中心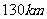 内的地方都要受到其影响。
内的地方都要受到其影响。
⑴台风中心在移动过程中,与气象台A的最短距离是多少?
 ⑵台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的实践会持续多长?
⑵台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的实践会持续多长?
25、(河北08)气象台发布的卫星云图显示,代号为W的台风在某海岛(设为点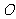 )的南偏东
)的南偏东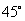 方向的
方向的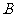 点生成,测得
点生成,测得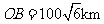 .台风中心从点
.台风中心从点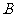 以40km/h的速度向正北方向移动,经5h后到达海面上的点
以40km/h的速度向正北方向移动,经5h后到达海面上的点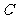 处.因受气旋影响,台风中心从点
处.因受气旋影响,台风中心从点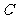 开始以30km/h的速度向北偏西
开始以30km/h的速度向北偏西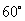 方向继续移动.以
方向继续移动.以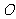 为原点建立如图所示的直角坐标系.
为原点建立如图所示的直角坐标系.
(1)台风中心生成点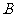 的坐标为
,台风中心转折点
的坐标为
,台风中心转折点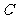 的坐标为
;(结果保留根号)
的坐标为
;(结果保留根号)
 (2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点
(2)已知距台风中心20km的范围内均会受到台风的侵袭.如果某城市(设为点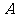 )位于点
)位于点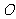 的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
24、(河北07)某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60 km/h(即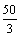 m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
m/s).交通管理部门在离该公路100 m处设置了一速度监测点A,在如图所示的坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.
(1)请在图中画出表示北偏东45°方向的射线AC,并标出点C的位置;
(2)点B坐标为 ,点C坐标为 ;
 (3)一辆汽车从点B行驶到点C所用的时间为15 s,请通过计算,判断该汽车在限速公路上是否超速行驶?(本小问中
(3)一辆汽车从点B行驶到点C所用的时间为15 s,请通过计算,判断该汽车在限速公路上是否超速行驶?(本小问中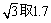 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com