⒈内容：一切物体总保持______________状态或____________，除非作用在它上面的力迫使它____________________。

⒉意义：

①指出力不是____________物体运动的原因，而是____________物体运动状态的原因，即力是使产生______________的原因。

②指出了一切物体________________________，因此牛顿第一定律又称_______________。

⒊惯性：

①定义：物体具有保持原来______________状态或____________状态的性质。

②量度：____________是物体惯性大小的唯一量度(在牛顿第一定律中没指出惯性大小如何量度)

③普遍性：惯性是物体的____________属性，一切物体都有惯性。

④表现：物体的惯性总以保持原状或反抗改变(运动状态改变的难易程度)两种形式表现出来，与物体是否受力、怎样受力无关。

　　 《课课练》　 P51-54中有关值域部分

　　 《教学与测试》　 P41-42中有关值域部分

4．换元法：注意“新元”的取值范围

3．△法：须检验

2．二次函数法：应特别当心“定义域”

1．直接法：应注意基本初等函数的值域

解：设 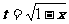　则 t≥0 　　x=1-t²

　 　　　　代入得 y=f (t )=2×(1-t²)+4t=-2t²+4t+2=-2(t-1)²+4

　　　　 ∵t≥0　　 ∴y≤4

　　 　解一：去分母得　 (y-1)x²+(y+5)x-6y-6=0　　 (*)

　　 　　　　当 y¹1时　 ∵xÎR　 ∴△=(y+5)²+4(y-1)×6(y+1)≥0

　　 　　　　　　　　由此得 (5y+1)²≥0

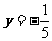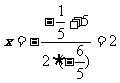检验 　时　 (代入(*)求根)

　 　　　　　　　∵2Ï定义域 { x| x¹2且 x¹3}　　 ∴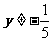

再检验 y=1 代入(*)求得 x=2　　 ∴y¹1

综上所述，函数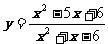的值域为 { y| y¹1且 y¹}

解二：把已知函数化为函数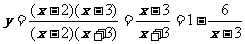　 (x¹2)　 由此可得 y¹1

　 　　　　　∵x=2时　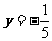 　　即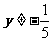

　　　　　　 ∴函数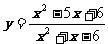的值域为 { y| y¹1且 y¹}

4．换元法

　　 解：由题设 x≥0 　y=x²+2x+3=(x+1)²+2

　　　　 当 x=0 时 y_min=3　 函数无最大值　 　

∴函数 y=x²+2x+3的值域是{ y| y≥3}

　 　　　2°求函数 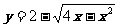的值域

　　 　解：由 4x-x²≥0 得 0≤x≤4

　在此区间内　 (4x-x²)_max=4　　 (4x-x²)_min=0

∴函数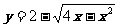的值域是{ y| 0≤y≤2}

3．判别式法(△法)

解：1° 　　∵　　 ∴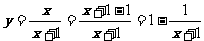

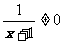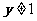
　　 　　　即函数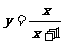的值域是 { y| yÎR且y¹1}　

(此法亦称部分分式法)

　　 　　2° 　　　∵　　 ∴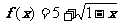

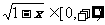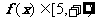
　　 　　　即函数y =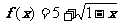的值域是 { y| y≥5}

2．二次函数法：