1．复数=　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )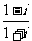

　 　　　 A．i　　　　　 　　　　 B．-i　 　　　　　　　　　 C．l　　　　 　　　　　 D．-1

22．(本小题满分14分)

已知函数f(x)= ax +lnx，a∈R．

　 (I)求函数f(x)的极值；

　 (II)对于曲线上的不同两点P₁( x₁，y₂)，P₂(x₂，y₂)，如果存在曲线上的点Q( x₀，y₀)，且x₁<x₀<x₂，使得曲线在点Q处的切线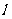∥P₁P₂，则称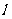为弦P₁P₂的伴随切线，求证：曲线y=f(x)的任意一条弦均有伴随切线，并且伴随切线是唯一的。

21．(本小题满分12分)

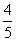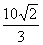已知焦点在x轴上，中心在坐标原点的椭圆c的离心率为，且过点(，1)．

(I)求椭圆C的方程；

(Ⅱ)直线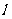：y=kx +m分别切椭圆C与圆M:x² +y²= 15于A、B两点，求|AB|的值．

20．(本小题满分12分)

如图，等腰梯形ABEF中，AB∥EF，AB =2，AD=AF=1，AF⊥BF，O为AB的中点，矩形ABCD所在的平面和平面ABEF互相垂直．

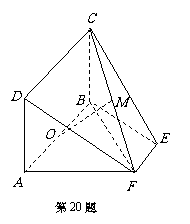(I)求证：AF⊥平面CBF；

(Ⅱ)设FC的中点为M，求证：OM∥平面DAF;

(Ⅲ)求三棱锥C - BEF的体积．

19．(本小题满分12分)

已知函数f(x)= 2asinωxcosωx+2bcos²ωx－b(a、b、ω>0)在x=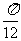时取最大值2．x_l，x₂是集合M={x∈R|f(x) =0}中的任意两个元素，|x₁- x₂|的最小值为。

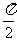　 (I)求a、b的值；

　 (II)若f(α)=2/3，求sin(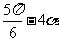)的值．

18．(本小题满分12分)

已知数列{a_n}的首项a₁=a,an=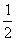a_n-1．+l(n∈N*，n≥2)，若b_n =a_n一2(n∈N*)

　 (I)问数列{b_n}是否构成等比数列，并说明理由；

　 (II)若已知a₁=1，设数列{a_n，b_n}的前n项和为S_n，求S_n．

17．(本小题满分12分)

联合国准备举办一次有关全球气候变化的会议，分组研讨时某组有6名代表参加，A、B两名代表来自亚洲，C、D两名代表来自北美洲，E、F两名代表来自非洲，小组讨论后将随机选出两名代表发言．

　 (I)代表A被选中的概率是多少？

　 (II)选出的两名代表“恰有1名来自北美洲或2名都来自非洲”的概率是多少？

15．已知过双曲线等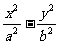=l右焦点且倾斜角为45°的直线与双曲线右支有两个交点，则双曲线的离心离e的取值范围是__________________________。

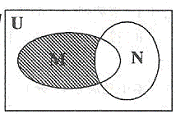
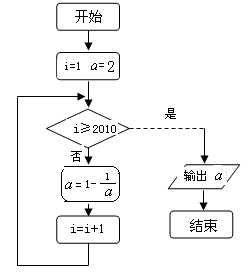
14．已知某程序框图如图所示，则执行该程序后输出的结果是_________________________。