
3.幂函数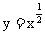 的性质.
的性质.
[作业布置]:课本习题:3-3 A组 1-7
2.掌握不同底的指数函数的大小比较关系.
1.利用指数函数的单调性比较两个数的大小关系.
3、情感.态度与价值观
使学生通过学习指数函数的图像,了解到指数函数具有的性质.在学习的过程中体会研究具体函数及其性质的过程和方法,如具体到一般的过程、数形结合的方法等,增强学习指数函数的积极性和自信心.
[教学重点]: 指数函数的图像和性质.
[教学难点]:指数函数的图像和性质与底数的关系
[学法指导]:学生思考、探究.
[讲授过程]
[新课导入]
[互动过程1]
复习:指数函数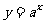 在底数
在底数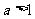 及
及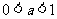 这两种情况下的图像和性质:
这两种情况下的图像和性质: 
|
|
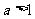 |
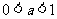 |
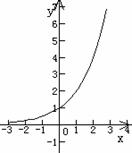
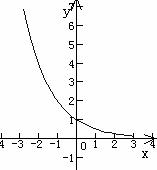
  图象   |
 |
 |
|
性质 |
(1)定义域: |
|
(2)值域: |
||
(3)过点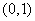 ,即 ,即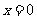 时 时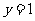 |
||
|
当x>0时,y>1;当x<0时,0<y<1 |
当x>0时, 0<y<1;当x<0时, y>1 |
|
(4)在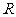 上是增函数 上是增函数 |
(4)在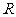 上是减函数 上是减函数 |
练习1:比较下列数的大小关系:(1)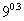 与
与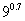 ;(2)
;(2)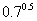 与
与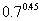

[互动过程2]
根据指数函数的性质,我们就可以解方程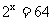 .你能解指数不等式吗?怎样解?
.你能解指数不等式吗?怎样解?
例2(1)求不等式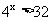 成立的x的集合;(2)已知
成立的x的集合;(2)已知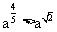 ,求数a的取值范围.
,求数a的取值范围.
分析:对于指数不等式,即比较不等式左右两边数的大小,可以把两边的数化为同底数,根据指数函数的单调性比较出来,也可以直接利用计算器算出数值进行比较.
解:(1)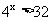 即为
即为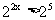 ,因为
,因为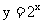 在R上是增函数,所以
在R上是增函数,所以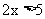 ,
,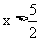 .所以满足
.所以满足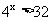 的x的集合为
的x的集合为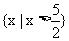 .
.
(2)由于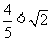 且
且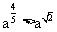 ,所以函数
,所以函数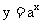 为减函数,所以
为减函数,所以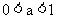 .
.
练习2:(1)求不等式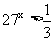 成立的x的集合;(2)已知
成立的x的集合;(2)已知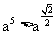 ,求数a的取值范围.
,求数a的取值范围.
解:(1)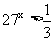 即为
即为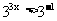 ,因为
,因为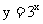 在R上是增函数,所以
在R上是增函数,所以 ,
,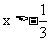 .所以满足
.所以满足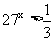 的x的集合为
的x的集合为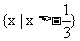 .
.
 (2)由于
(2)由于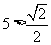 且
且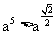 ,所以函数
,所以函数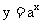 为增函数,所以
为增函数,所以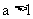 .
.
[互动过程3]
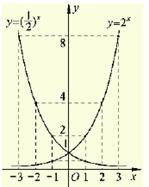
例3.请你在同一坐标系中画出函数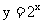 和
和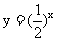 的图像,说出其
的图像,说出其
自变量,函数值及其图象间的关系.
解:在同一坐标系中画出函数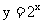 和
和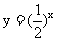 的图像如图所示,
的图像如图所示,
从图中可以看出,当函数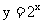 和函数
和函数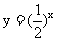 的自变量的取值
的自变量的取值
互为相反时,其函数值是相等的,因而两个函数的图像关于y轴对称.
猜想:函数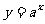 与
与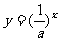 的图像之间有什么关系?能说明吗?
的图像之间有什么关系?能说明吗?
分析:函数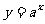 图像上的点
图像上的点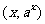 关于y轴对称的点
关于y轴对称的点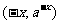 ,该点坐标还可可表示为
,该点坐标还可可表示为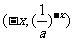 在
在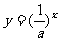 的图像上;
的图像上;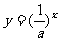 图像上的点
图像上的点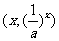 关于Y轴对称的点
关于Y轴对称的点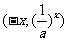 ,该点坐标还可可表示为
,该点坐标还可可表示为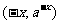 在
在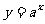 图像上。因此,猜想函数
图像上。因此,猜想函数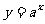 与
与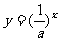 关于y轴对称是正确的。
关于y轴对称是正确的。
结论1:
一般地,当函数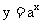 和函数
和函数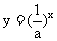 ,即函数
,即函数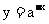 的自变量的取值互为相反数时,其函数值是相等的,这两个函数的图像是关于y轴对称的.
的自变量的取值互为相反数时,其函数值是相等的,这两个函数的图像是关于y轴对称的.
练习3:请你在同一坐标系中画出函数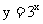 和
和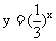 的图像.
的图像.
[互动过程4]
指数函数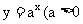 且
且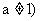 中,底数
中,底数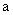 对函数图像有什么影响?请同学们在同一指教坐标系中画出函数
对函数图像有什么影响?请同学们在同一指教坐标系中画出函数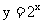 和函数
和函数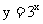 的图象,比较两个函数增长的快慢.
的图象,比较两个函数增长的快慢.
|
x |
…
|
-2
|
-1
|
0
|
1
|
2
|
3
|
…
|
10
|
…
|
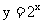 |
…
|
0.25
|
0.5
|
1
|
2
|
4
|
8
|
…
|
1024
|
…
|
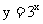 |
…
|
0.11
|
0.33
|
1
|
3
|
9
|
27
|
…
|
59049
|
…
|
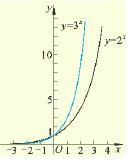 从表或图象可以看出
从表或图象可以看出
(1)当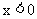 时,总有
时,总有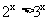 ;
;
(2)当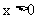 时,总有
时,总有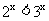 ;
;
(3)当从0增加到10,函数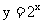 的函数值从1增加到1024,函数
的函数值从1增加到1024,函数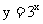
的函数值从1增加到59049.这说明,当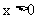 时,函数
时,函数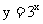 的函数值比函数
的函数值比函数
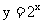 的函数值增长得快.
的函数值增长得快.
结论2:一般地,当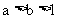 时,
时,
(1)当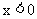 时,总有
时,总有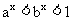 ;
;
(2)当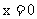 时,总有
时,总有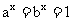 ;
;
(3)当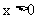 时,总有
时,总有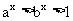 ;
;
(4)指数函数的底数越大,当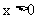 时,其函数值增长得就越快.
时,其函数值增长得就越快.
 [互动过程5]
[互动过程5]
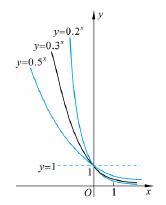
请同学们分别画出底数为0.2,0.3,0.5的指数函数的图象,
想像底数为2,3,5时指数函数的图象,研究指数函数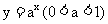
中,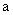 对函数图象变化的影响.
对函数图象变化的影响.
观察图形,请你总结出函数图象随着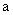 变化的规律是什么?
变化的规律是什么?
当字变量取同一数值时,比较对应函数值的大小,你能发现什么规律?
结论3:一般地,当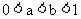 时,
时,
(1)当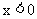 时,总有
时,总有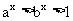 ;
;
(2)当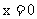 时,总有
时,总有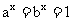 ;
;
(3)当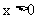 时,总有
时,总有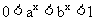 ;
;
(4)指数函数的底数越大,当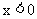 时,其函数值减少得就越缓慢.
时,其函数值减少得就越缓慢.
例4.比较下列各题中的两个数的大小:
(1)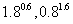 ;(2)
;(2)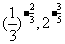 .
.
解:方法一:直接用科学计算器计算各数的值,再对两个数进行比较大小.
(1)因为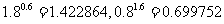 ,所以
,所以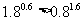 ;
;
(2)因为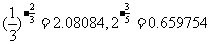 ,所以
,所以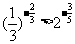
方法二:利用指数函数的性质对两个数值进行比较大小.
(1).由指数函数的性质知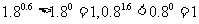 ,所以
,所以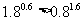
(2).由指数函数的性质知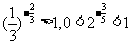 ,所以
,所以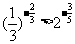 .
.
练习4.比较下列各题中的两个数的大小:
(1)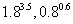 ;(2)
;(2)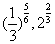 .
.
例5.已知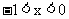 ,比较
,比较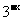 ,
,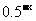 的大小,并说明理由.
的大小,并说明理由.
解:因为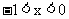 ,所以
,所以 .而
.而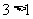 ,因此有
,因此有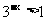 ,又
,又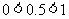 ,所以有
,所以有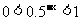 ,所以
,所以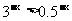 .
.
练习5:已知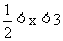 ,比较
,比较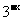 ,
,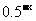 的大小,并说明理由.
的大小,并说明理由.
[互动过程6]
我们已经把整数指数幂扩充到有理指数幂,前面学习过的幂函数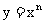 中的指数
中的指数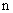 也可以扩充到有理数.下面讨论有理数指数幂
也可以扩充到有理数.下面讨论有理数指数幂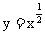 的性质.
的性质.
列出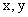 的对应值;用描点的方法,画出函数
的对应值;用描点的方法,画出函数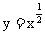 的图像
的图像
|
x |
0
|
0.5
|
1
|
2
|
3
|
4
|
…
|
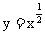
|
0
|
0.71
|
1
|
1.41
|
1.73
|
2
|
…
|
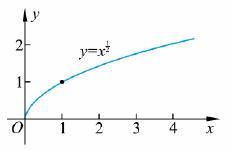
它的性质:(1)函数定义在区间 上,值域是
上,值域是 ;
;
(2)图像过点(0,0),(1,1);
(3)函数是增函数.
练习6.若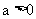 ,比较
,比较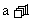 与
与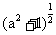 的大小关系.
的大小关系.
[课堂小结]:
2、 过程与方法 
(1)让学生掌握指数函数的图像和性质,进一步体会指数函数的性质与底数的关系.
(2)通过特殊到一般的研究方法研究一个陌生问题是一种常规的思维方式,是由表及里的上升循环过程,学习指数函数的性质是为了更好的研究具体函数.
1、知识与技能
(1)进行学习指数函数的图像和性质,并用来解答.
(2)能够画出指数函数的图像,总结出指数函数的性质,并通过图像和性质比较指数的大小和解简单的指数不等式.
22.(本题满分14分)
设数列{an}的前n项和为Sn若a1=1,a2=6,a3=11,且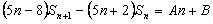 (n=1,2,3,……) 其中A、B为常数
(n=1,2,3,……) 其中A、B为常数
(1)求A、B的值;
(2)证明:{an}为等差数列;
(3)证明:不等式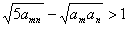 对任何正整数m、n都成立.
对任何正整数m、n都成立.

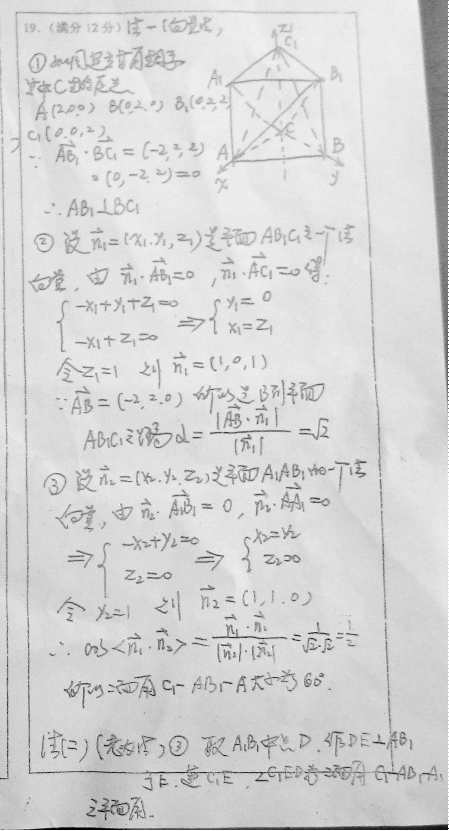

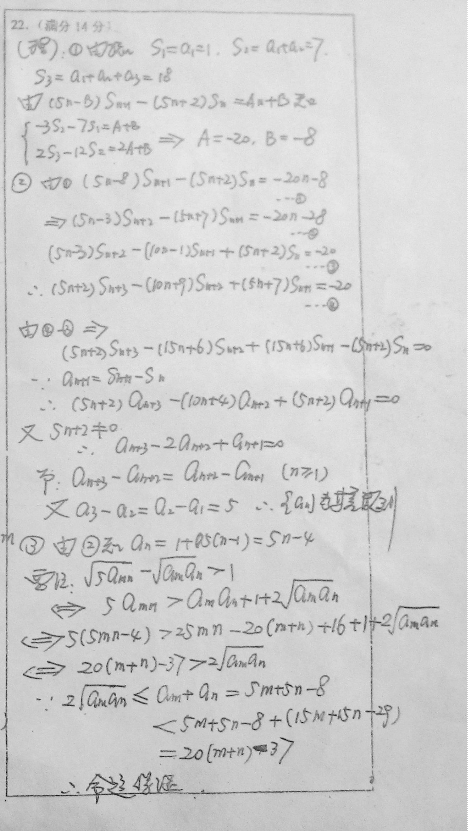
21.(本题满分12分)
如图:线段AB过x轴上一点M(m,0) (m>0),端点A、B到x轴距离之积为3m,以x轴为对称轴,过A、O、B三点作抛物线.
(1)求抛物线方程;
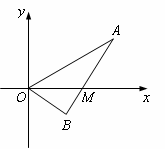 (2)若直线AB斜率为
(2)若直线AB斜率为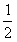 ,求当0<m<3时,∠AOB的取值范围.
,求当0<m<3时,∠AOB的取值范围.
20.(本题满分12分)
曲线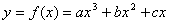 ,当
,当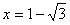 时f(x)有极小值;当
时f(x)有极小值;当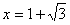 有极大值,且在x=1处切线斜率为
有极大值,且在x=1处切线斜率为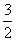 .求:
.求:
(1)f(x)=?
(2)曲线上是否存在一点P使得y=f(x)的图象关于点P成中心对称?若存在,请求出点P坐标,并给出证明;若不存在,说明理由.
19.(本题满分12分)
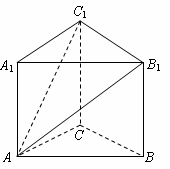
如图:在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(1)求证:AB1⊥BC1;
(2)求点B到平面AB1C1之距离;
(3)求二面角C1-AB1-A1之大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com