
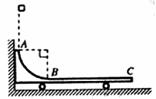
9.(2010年韶关一模)(18分)如图所示,水平光滑地面上停放着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径的10倍,整个轨道处于同一竖直平面内.可视为质点的物块从A点正上方某处无初速下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道滑行至轨道末端C处恰好没有滑出.已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,小车的质量是物块的3倍,不考虑空气阻力和物块落入圆弧轨道时的能量损失.求:
 (1)物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍
(1)物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍
(2)物块与水平轨道BC间的动摩擦因数μ
[解析](1)设物块的质量为m,其开始下落处的位置距BC的竖直高度为h,到达B点时的速度为v,小车圆弧轨道半径为R.
由机械能守恒定律,有:mgh=mv2 4分
根据牛顿第二定律,有:9mg-mg=m 4分
解得: h=4R 1分
则物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍.
(2)设物块与BC间的滑动摩擦力的大小为F,物块滑到C点时与小车的共同速度为v',物块在小车上由B运动到C的过程中小车对地面的位移大小为s.依题意,小车的质量为3m,BC长度为10R.
由滑动摩擦定律有: F=μmg 2分
由动量守恒定律,有mv=(m+3m)v' 2分
对物块、小车分别应用动能定理,有
-F(10R+s)=mv'2 -mv2 2分
Fs=(3m)v'2-0 2分
μ=0.3
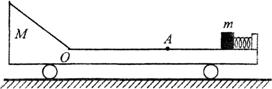
8.(2010年湛江一模)(20分)如图所示,光滑水平面上有一长板车,车的上表面0A段是一长为己的水平粗 糙轨道,A的右侧光滑,水平轨道左侧是一光滑斜面轨道,斜面轨道与水平轨道在O点平 滑连接。车右端固定一个处于锁定状态的压缩轻弹簧,其弹性势能为Ep,一质量为m的小物体(可视为质点)紧靠弹簧,小物体与粗糙水平轨道间的动摩擦因数为μ,整个装置处于静止状态。现将轻弹簧解除锁定,小物体被弹出后滑上水平粗糙轨道。车的质量为 2m,斜面轨道的长度足够长,忽略小物体运动经过O点处产生的机械能损失,不计空气阻力。求:
(1)解除锁定结束后小物体获得的最大动能;
(2)当∥满足什么条件小物体能滑到斜面轨道上,满足此条件时小物体能上升的最 大高度为多少?
[解析](1)设解锁弹开后小物体的最大速度饷大小为v1,小物体的最大动啦为Ek ,此时长板车的速度大小为v2,研究解锁弹开过程小物体和车组成的系统,根据动量守恒和机械能守恒,有 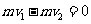 ①(2分)
①(2分)
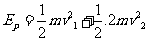 ②(3分)
②(3分)
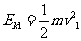 ③(1分)
③(1分)
联立①②③式解得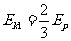 ④(2分)
④(2分)
(2)小物体相对车静止时,二者有共同的速度设为V共,长板车和小物体组成的系统水平方向动量守恒 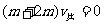 ⑤(2分)
⑤(2分)
所以v共=0 ⑥(1分)
要使小物体能滑上斜面轨道,:必须满足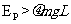 ;⑦( 3分)
;⑦( 3分)
即当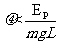 时,小物体能滑上斜面轨道⑧ (1分)
时,小物体能滑上斜面轨道⑧ (1分)
设小物体上升的最大高度为h,此瞬间小物体相对车静止,由⑤式知两者有共同速度为零.⑨(1分)
根据系统能量守恒有
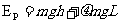 ⑩(3分)
⑩(3分)
解得: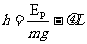 (1分)
(1分)
7.(2010年汕头一模)(18分)如图所示,在倾角θ=30º的斜面上放置一段凹槽B,B与斜面间的动摩擦因数μ=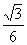 ,槽内靠近右侧壁处有一小球A,它到凹槽内左壁侧的距离d=0.10m.A、B的质量都为m=2.0kg,B与斜面间的最大静摩擦力可认为等于滑动摩擦力,不计A、B之间的摩擦,斜面足够长.现同时由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞,碰撞过程不损失机械能,碰撞时间极短.取重力加速度g=10m/s2.求:
,槽内靠近右侧壁处有一小球A,它到凹槽内左壁侧的距离d=0.10m.A、B的质量都为m=2.0kg,B与斜面间的最大静摩擦力可认为等于滑动摩擦力,不计A、B之间的摩擦,斜面足够长.现同时由静止释放A、B,经过一段时间,A与B的侧壁发生碰撞,碰撞过程不损失机械能,碰撞时间极短.取重力加速度g=10m/s2.求:
(1)A与B的左侧壁第一次发生碰撞后瞬间A、B的速度.
 (2)在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内,A与B的左侧壁的距离最大可达到多少?
(2)在A与B的左侧壁发生第一次碰撞后到第二次碰撞前的这段时间内,A与B的左侧壁的距离最大可达到多少?
[解析](1)A在凹槽内,B受到的滑动摩擦力
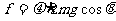 =10N
①(1分)
=10N
①(1分)
B所受重力沿斜面的分力
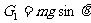 =10N
=10N
因为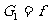 ,所以B受力平衡,释放后B保持静止 ②(1分)
,所以B受力平衡,释放后B保持静止 ②(1分)
释放A后,A做匀加速运动,由牛顿定律和运动学规律得
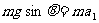 ③(1分)
③(1分)
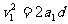 ④(1分)
④(1分)
解得A的加速度和碰撞前的速度分别为
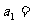 5m/s2,
5m/s2,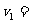 1.0 m/s
⑤(1分)
1.0 m/s
⑤(1分)
A、B发生碰撞,动量守恒
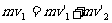 ⑥(2分)
⑥(2分)
碰撞过程不损失机械能,得
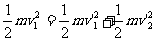 ⑦(1分)
⑦(1分)
解得第一次发生碰撞后瞬间A、B的速度分别为
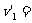 0,
0,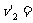 1.0 m/s(方向沿斜面向下) ⑧(2分)
1.0 m/s(方向沿斜面向下) ⑧(2分)
(2)A、B第一次碰撞后,B做匀速运动
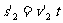 ⑨(1分)
⑨(1分)
A做匀加速运动,加速度仍为a1
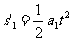 ⑩(1分)
⑩(1分)
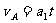 ⑾(1分)
⑾(1分)
经过时间t1,A的速度与B相等,A与B的左侧壁距离达到最大,即
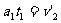 ⑿(1分)
⑿(1分)
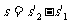 ⒀(1分)
⒀(1分)
代入数据解得A与B左侧壁的距离
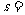 0.10m
⒁(2分)
0.10m
⒁(2分)
因为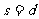 , A恰好运动到B的右侧壁,而且速度相等,所以A与B的右侧壁恰好接触但没有发生碰撞。
⒂(1分)
, A恰好运动到B的右侧壁,而且速度相等,所以A与B的右侧壁恰好接触但没有发生碰撞。
⒂(1分)
因此A与B的左侧壁的距离最大可达到0.10m。
5.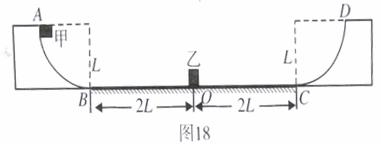 (2010年广州一模)(18分)如图18所示的凹形场地,两端是半径为L的1/4圆弧面,中间是长尾4L的粗糙水平面。质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内并与乙发生碰撞,碰后以碰前一半的速度反弹。已知甲、乙与水平面的动摩擦因数分别为μ1、μ2,且μ1=2μ2,甲、乙的体积大小忽略不计。求:
(2010年广州一模)(18分)如图18所示的凹形场地,两端是半径为L的1/4圆弧面,中间是长尾4L的粗糙水平面。质量为3m的滑块乙开始停在水平面的中点O处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内并与乙发生碰撞,碰后以碰前一半的速度反弹。已知甲、乙与水平面的动摩擦因数分别为μ1、μ2,且μ1=2μ2,甲、乙的体积大小忽略不计。求:
(1)甲与乙碰撞前的速度。
(2)碰后瞬间乙的速度。
(3)甲、乙在O处发生碰撞后,
刚好不再发生碰撞,则甲、乙停在
距B点多远处。
[解析](1)设甲到达O处与乙碰撞前的速度为v甲,由动能定理:
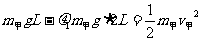 ……2分
……2分
得: 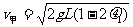 ……2分
……2分
(分步用机械能守恒和匀减速直线运动进行计算,结果正确的同样给4分)
(2)设碰撞后甲、乙的速度分别为v甲′、v乙′,由动量守恒:
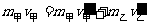 ……2分
……2分
又: 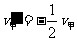 ……1分
……1分
得: 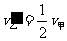 ……1分
……1分
(3)由于μ1=2μ2,所以甲、乙在水平面上运动的加速度满足:a甲=2a乙 ……1分
设甲在水平地面上通过的路程为s1、乙在水平地面上通过的路程为s2,则有:
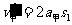 ……1分
……1分
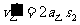 ……1分
……1分
即: 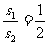 ① ……1分
① ……1分
由于甲、乙刚好不再发生第二次碰撞,所以甲、乙在同一地点停下.有以下两种情况:
第一种情况:甲返回时未到达B时就已经停下,此时有:s1<2L ……1分
而乙停在甲所在位置时,乙通过的路程为:s2=2L+2L+s1=4L+s1 ……1分
因为s1与s2不能满足①,因而这种情况不能发生. ……1分
第二种情况:甲、乙分别通过B、C冲上圆弧面后,返回水平面后相向运动停在同一地点,所以有:s1+s2=8L ② ……1分
①②两式得: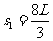 或
或 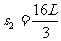 ……1分
……1分
即小车停在距B为: 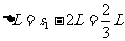 ……1分
……1分
(评分说明:第(3)问如果没有进行分类讨论,直接认为是第二种情况且结果正确的只给5分)
5.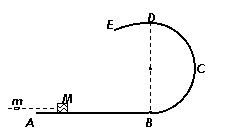 (2010年3月深圳一模)(18分)如图所示, ABCDE是由三部分光滑轨道平滑连接在一起组成的,AB为水平轨道,
(2010年3月深圳一模)(18分)如图所示, ABCDE是由三部分光滑轨道平滑连接在一起组成的,AB为水平轨道, 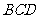 是半径为R的半圆弧轨道,
是半径为R的半圆弧轨道,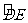 是半径为2R的圆弧轨道,BCD
是半径为2R的圆弧轨道,BCD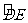 相切在轨道最高点D,R=0.6m.质量为M=0.99 kg的小物块,静止在AB轨道上,一颗质量为m=0.01kg子弹水平射入物块但未穿出,物块与子弹一起运动,恰能贴着轨道内侧通过最高点从E点飞出.取重力加速度g=10m/s2,求:
相切在轨道最高点D,R=0.6m.质量为M=0.99 kg的小物块,静止在AB轨道上,一颗质量为m=0.01kg子弹水平射入物块但未穿出,物块与子弹一起运动,恰能贴着轨道内侧通过最高点从E点飞出.取重力加速度g=10m/s2,求:
(1)物块与子弹一起刚滑上圆弧轨道B点的速度;
(2)子弹击中物块前的速度;
(3)系统损失的机械能.
解析:(1)由物块与子弹一起恰能通过轨道最高点D,得:
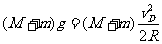 (3分)
(3分)
又由物块与子弹上滑过中根据机械能守恒得:
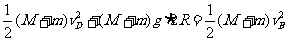 (3分)
(3分)
代入数据解得: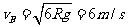 (2分)
(2分)
(2)由动量守恒 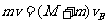 (3分)
(3分)
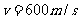 (2分)
(2分)
(3)根据能的转化和守恒定律得 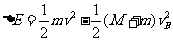 (3分)
(3分)
代入数据得: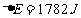 (2分)
(2分)
4.(2010年1月广州市调研题)如右图所示,在光滑水平面上质量分别为mA=2kg、mB=4kg,速率分别为vA=5m/s、vB=2m/s的A、B两小球沿同一直线相向运动 C
 A.它们碰撞前的总动量是18kg·m/s,方向水平向右
A.它们碰撞前的总动量是18kg·m/s,方向水平向右
B.它们碰撞后的总动量是18kg·m/s,方向水平向左
C.它们碰撞前的总动量是2kg·m/s,方向水平向右
D.它们碰撞后的总动量是2kg·m/s,方向水平向左
[解析]以向右右方为正向,由动量守恒可知总动量为2kg·m/s,方向水平向右,C正确
3.(2010年1月肇庆一模21)质量为M的小车中挂有一个单摆,摆球的质量为M0,小车和单摆以恒定的速度V0沿水平地面运动,与位于正对面的质量为M1的静止木块发生碰撞,碰撞时间极短,在此过程中,下列哪些说法是可能发生的 BC
A.小车、木块、摆球的速度都发生变化,分别为V1、V2和V3,且满足:
(M+M0)V0=MV1+M1V2+M0V3;
B.摆球的速度不变,小车和木块的速度为V1、V2,且满足:MV0=MV1+M1V2;
C.摆球的速度不变,小车和木块的速度都为V,且满足:MV0=(M+M1)V;
D.小车和摆球的速度都变为V1,木块的速度变为V2,且满足:(M+M0)V0=(M+M0)V1+M1V2
[解析]碰撞时间极短,单摆速度来不及改变,小车和木箱组成的系统动量守恒,碰撞前后的动能关系,可知BC正确
2.(2010年1月广东六校联考)(18分)如图,在光滑水平长直轨道上有A、B两个绝缘体,它们之间有一根长L的轻质细线相连接,其中A的质量为m,B的质量为M=2m,A为带有电量为+q的物体,B不带电,空间存在着方向水平向右的匀强电场,电场强度为E。开始时用外力把A与B靠在一起并保持静止,某时刻撤去外力,A开始向右运动,直到细线绷紧。当细线被绷紧时,细线存在极短时间的弹力,而后B开始运动。已知B开始运动时的速度等于线刚绷紧前瞬间A的速度的1/2,设整个过程中,A的电荷量保持不变。求:
(1)B开始运动时,A运动的速度
(2)通过计算来判断细线在第二次绷紧前A、B是否发生碰撞
(3)在(2)中,若A、B发生碰撞,求碰撞前瞬间B的位移;若A、B不发生碰撞,求细线第二次绷紧前瞬间B的位移
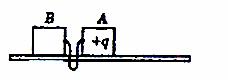
[解析](1)从运动到拉直时,A的速度为v0 ,则:
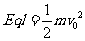 解得:
解得: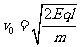 (3分)
(3分)
绷紧前后,系统动量守恒,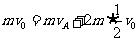 解得:
解得: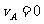 (3分)
(3分)
(2)第一次绷紧后,A作初速度为0的匀加速直线运动,B作0.5v0的匀速直线运动。
现假设二者能碰撞,B追上A的时间为t,则须同时满足下面两个条件:
1 二者能相遇 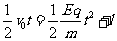 且t有实数解 (3分)
且t有实数解 (3分)
2 相遇时后面速度比前面大 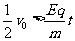 (3分)
(3分)
由1得到一元二次方程的判别式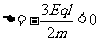 故t无实数解,说明B追不上A,也就没有2式成立。所以,二者不会发生碰撞。
(2分)
故t无实数解,说明B追不上A,也就没有2式成立。所以,二者不会发生碰撞。
(2分)
(3)设第二次绷紧时间为t2 则有:
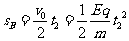 解得:
解得: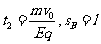 (4分)
(4分)
如用其它方法来解,只要正确都给分。
1.(2010年1月惠州第三次调研20)如图所示,质量分别为m1和m2的两个小球A、B,带有等量异种电荷,通过绝缘轻弹簧相连接,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场后,两小球A、B将由静止开始运动,在以后的运动过程中,对两个小球和弹簧组成的系统(设整个过程中不考虑电荷间库仑力的作用且弹簧不超过弹性限度),以下说法正确的是AD
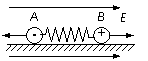 A.因电场力分别对球A和球B做正功,故系统机械能不断增加
A.因电场力分别对球A和球B做正功,故系统机械能不断增加
B.因两个小球所受电场力等大反向,故系统动量守恒
C.当弹簧长度达到最大值时,系统机械能最小
D.当小球所受电场力与弹簧的弹力相等时,系统动能最大
[解析]由功能关系知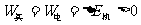 ,故A正确;对AB及弹簧组成的系统,水平方向上合外力为零,故动量守恒,B正确;当弹簧长度达到最大时,电场力做的功全转化为弹簧的弹性势能,机械能最大,C错;当A、B所受合力为零时,速度最大,动能最大,D正确
,故A正确;对AB及弹簧组成的系统,水平方向上合外力为零,故动量守恒,B正确;当弹簧长度达到最大时,电场力做的功全转化为弹簧的弹性势能,机械能最大,C错;当A、B所受合力为零时,速度最大,动能最大,D正确
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com