
3.设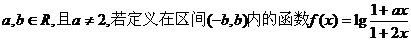 是奇函数,则
是奇函数,则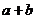 的取值范围是 ▲ .
的取值范围是 ▲ .
2.若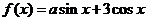 是偶函数,则实数
是偶函数,则实数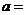 ▲
.
▲
.
1.设集合A={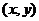 ︱
︱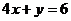 },B={
},B={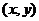 ︱
︱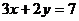 },则满足C
},则满足C (A∩B)的集合C的个数是 ▲
.
(A∩B)的集合C的个数是 ▲
.
20. (本小题共16分)已知函数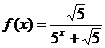 ,
,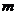 为正整数.
为正整数.
(Ⅰ)求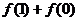 和
和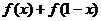 的值;
的值;
(Ⅱ)若数列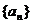 的通项公式为
的通项公式为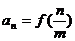 (
(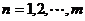 ),求数列
),求数列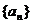 的前
的前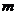 项和
项和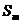 ;
;
(Ⅲ)设数列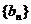 满足:
满足: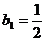 ,
,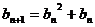 ,设
,设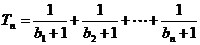 ,若(Ⅱ)中的
,若(Ⅱ)中的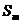 满足对任意不小于3的正整数n,
满足对任意不小于3的正整数n, 恒成立,试求m的最大值.
恒成立,试求m的最大值.
江苏省2010届苏北四市(徐州、宿迁、淮安、连云港)期末联考模拟试题(数学)
19.(本小题共16分) 已知二次函数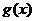 的图像经过坐标原点,且满足
的图像经过坐标原点,且满足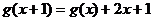 ,设函数
,设函数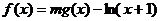 ,其中
,其中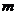 为非零常数
为非零常数
(I)求函数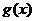 的解析式;
的解析式;
(II)当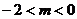 时,判断函数
时,判断函数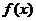 的单调性并且说明理由;
的单调性并且说明理由;
(III)证明:对任意的正整数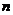 ,不等式
,不等式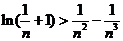 恒成立.
恒成立.
18. (本小题共16分)
已知直线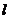 :
: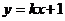 与圆C:
与圆C: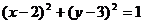 相交于
相交于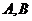 两点.
两点.
(Ⅰ)求弦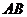 的中点
的中点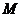 的轨迹方程;
的轨迹方程;
(Ⅱ)若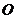 为坐标原点,
为坐标原点,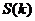 表示
表示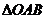 的面积,
的面积,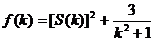 ,求
,求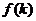 的最大值.
的最大值.
17. (本小题共14分)
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足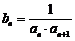 ,其前n项和为Sn.
,其前n项和为Sn.
(1)求数列{an}的通项公式an;
(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
16.(本小题共14分)
如图所示,在直三棱柱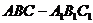 中,
中,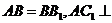 平面
平面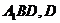 为
为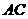 的中点.
的中点.
 (Ⅰ)求证:
(Ⅰ)求证: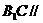 平面
平面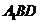 ;
;
(Ⅱ)求证: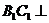 平面
平面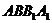 ;
;
(Ⅲ)设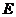 是
是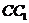 上一点,试确定
上一点,试确定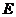 的位置使平面
的位置使平面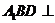 平面
平面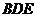 ,并说明理由.
,并说明理由.
15.(本小题共14分)已知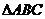 三个内角
三个内角 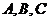 的对边分别为
的对边分别为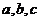 ,
, 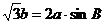 ,且
,且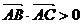 .
.
(Ⅰ)求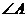 的度数;(Ⅱ)若
的度数;(Ⅱ)若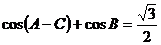 ,
, 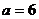 ,求
,求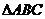 的面积.
的面积.
14.用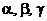 三个字母组成一个长度为
三个字母组成一个长度为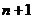
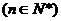 个字母的字符串,要求由
个字母的字符串,要求由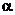 开始,相邻两个字母不同. 例如
开始,相邻两个字母不同. 例如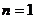 时,排出的字符串可能ks5是
时,排出的字符串可能ks5是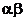 或
或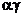 ;
;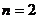 时排出的字符串可能是
时排出的字符串可能是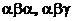 ,
,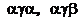 (如图).若记这种
(如图).若记这种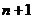 个字符串中,排在最后一个的字母仍是
个字符串中,排在最后一个的字母仍是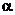 的所有字符串的种数为
的所有字符串的种数为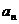 ,
可知,
,
可知,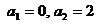 ;则
;则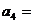 ▲ .数列
▲ .数列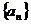 的前
的前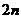 项之和
项之和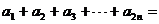 ▲ .
▲ .
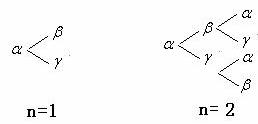
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com