
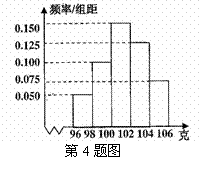
3.运行如图的算法,则输出的结果是 ▲ .

2.复数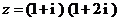 (
(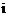 为虚数单位)的实部是 ▲ .
为虚数单位)的实部是 ▲ .
1.已知集合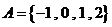 ,
,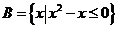 ,则
,则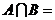 ▲ .
▲ .
23、已知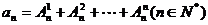 ,当
,当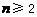 时,求证:
时,求证:
⑴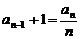 ;
;
⑵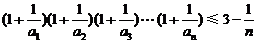
22、已知四棱锥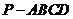 的底面
的底面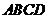 是直角梯形,
是直角梯形,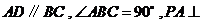 平面
平面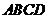 ,
,
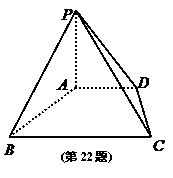
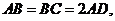 若平面
若平面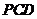 与平面
与平面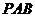 所成二面角的余弦值为
所成二面角的余弦值为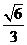 ,求
,求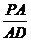 的值。
的值。
21、[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,共计20分。
A、(选修4-1.几何证明选讲)
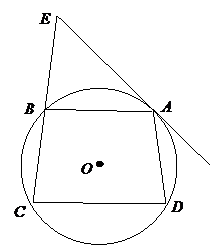 如图,四边形
如图,四边形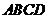 内接于圆O,弧AB=弧AD ,过
内接于圆O,弧AB=弧AD ,过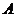 点的切线交
点的切线交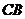 的延长线于
的延长线于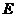 点。
点。
求证: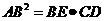
B、(选修4-2.矩阵与变换)
求曲线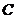 :
: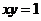 在矩阵
在矩阵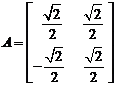 对应的变换下得到的曲线
对应的变换下得到的曲线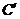 的方程。
的方程。
C、(选修4-4.坐标系与参数方程)
已知曲线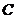 的极坐标方程为
的极坐标方程为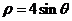 ,以极点为原点,极轴为
,以极点为原点,极轴为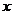 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线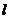 的参数方程为
的参数方程为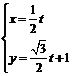 (
(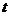 为参数),求直线
为参数),求直线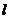 被曲线
被曲线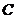 截得的线段长度。
截得的线段长度。
D、(选修4-5.不等式选讲)
已知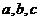 为正数,且满足
为正数,且满足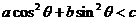 ,求证:
,求证: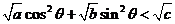
[必做题]每题10分,共20分
20. 设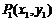 、
、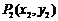 是函数
是函数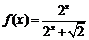 图象上的两点,且
图象上的两点,且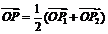 ,点P的横坐标为
,点P的横坐标为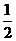 .(1)求证:P点的纵坐标为定值,并求出这个定值;(2)若
.(1)求证:P点的纵坐标为定值,并求出这个定值;(2)若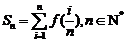 ,求
,求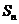 ;
;
(3)记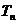 为数列
为数列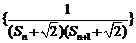 的前n项和,若
的前n项和,若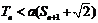 对一切
对一切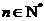 都成立,试求
都成立,试求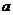 的取值范围.
的取值范围.
附加题
19.已知函数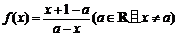 .
.
(1)当f(x)的定义域为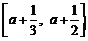 时,求f(x)的值域;
时,求f(x)的值域;
(2)求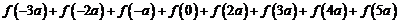 的值;
的值;
(3)设函数g(x)=x2+|(x-a)·f(x)| , 求g(x) 的最小值.
18、某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1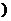 ,则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(Ⅰ)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(Ⅱ)年销售量关于x的函数为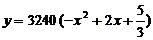 ,则当x为何值时,本年度的年利润最大?最大利润为多少?
,则当x为何值时,本年度的年利润最大?最大利润为多少?
17.若椭圆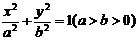 过点(-3,2),离心率为
过点(-3,2),离心率为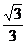 ,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为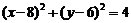 ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(I)求椭圆的方程;
(II)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;
(III)求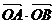 的最大值与最小值.
的最大值与最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com