
031]解:(1)5 , 24, 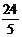 …………………………………3分
…………………………………3分
(2)①由题意,得AP=t,AQ=10-2t. ……………………………………1分
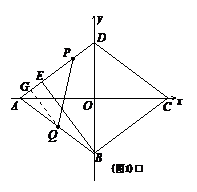 如图1,过点Q作QG⊥AD,垂足为G,由QG∥BE得 △AQG∽△ABE,∴
如图1,过点Q作QG⊥AD,垂足为G,由QG∥BE得 △AQG∽△ABE,∴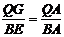 ,
,
∴QG=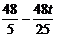 , …………………………1分
, …………………………1分
∴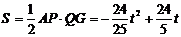 (
(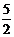 ≤t≤5).
≤t≤5).
∵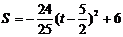 (
(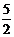 ≤t≤5).
≤t≤5).
∴当t=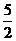 时,S最大值为6.…………………1分
时,S最大值为6.…………………1分
② 要使△APQ沿它的一边翻折,翻折前后的两个三角形组成的四边形为菱形,根据轴对称的性质,只需△APQ为等腰三角形即可.
当t=4秒时,∵点P的速度为每秒1个单位,∴AP=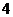 .………………1分
.………………1分
以下分两种情况讨论:
第一种情况:当点Q在CB上时, ∵PQ≥BE>PA,∴只存在点Q1,使Q1A=Q1P.
如图2,过点Q1作Q1M⊥AP,垂足为点M,Q1M交AC于点F,则AM=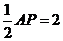 .
.
由△AMF∽△AOD∽△CQ1F,得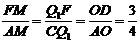 ,
, 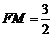 ,
,
∴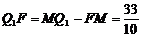 . ………………1分
. ………………1分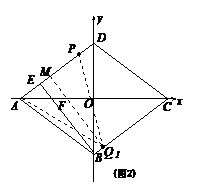 ∴CQ1=
∴CQ1=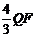 =
=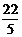 .则
.则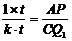 ,
,
∴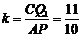 .……………………………1分
.……………………………1分
第二种情况:当点Q在BA上时,存在两点Q2,Q3,
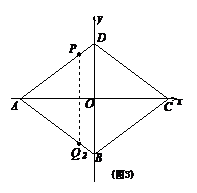 分别使A P= A
Q2,PA=PQ3.
分别使A P= A
Q2,PA=PQ3.
①若AP=AQ2,如图3,CB+BQ2=10-4=6.
则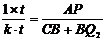 ,∴
,∴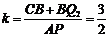 .……1分
.……1分
②若PA=PQ3,如图4,过点P作PN⊥AB,垂足为N,
由△ANP∽△AEB,得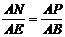 .
.
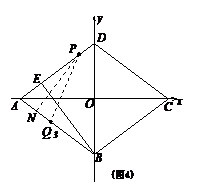 ∵AE=
∵AE=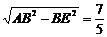 , ∴AN=
, ∴AN=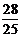 .
.
∴AQ3=2AN=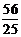 , ∴BC+BQ3=10-
, ∴BC+BQ3=10-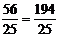
则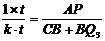 .∴
.∴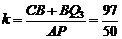 .
.
………………………1分
综上所述,当t= 4秒,以所得的等腰三角形APQ沿底边翻折,翻折后得到菱形的k值为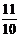 或
或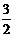 或
或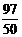 .
.
040]△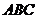 与△
与△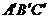 是两个直角边都等于
是两个直角边都等于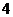 厘米的等腰直角三角形,M、N分别是直角边AC、BC的中点。△
厘米的等腰直角三角形,M、N分别是直角边AC、BC的中点。△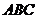 位置固定,△
位置固定,△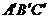 按如图叠放,使斜边
按如图叠放,使斜边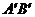 在直线MN上,顶点
在直线MN上,顶点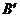 与点M重合。等腰直角△
与点M重合。等腰直角△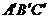 以1厘米/秒的速度沿直线MN向右平移,直到点
以1厘米/秒的速度沿直线MN向右平移,直到点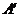 与点N重合。设
与点N重合。设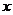 秒时,△
秒时,△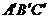 与△
与△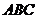 重叠部分面积为
重叠部分面积为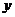 平方厘米。
平方厘米。
(1)当△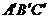 与△
与△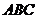 重叠部分面积为
重叠部分面积为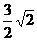 平方厘米时,求△
平方厘米时,求△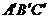 移动的时间;
移动的时间;
(2)求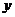 与
与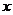 的函数关系式;
的函数关系式;
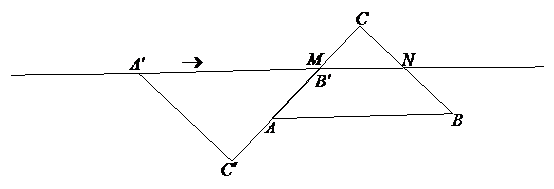 (3)求△
(3)求△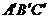 与△
与△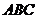 重叠部分面积的最大值。
重叠部分面积的最大值。


039]如图,已知点A(-4,8)和点B(2,n)在抛物线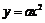 上.
上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线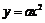 ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
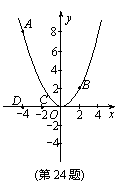
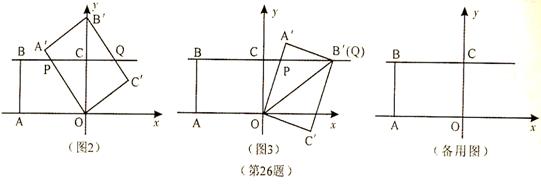
038]如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时声母OA′、直线B′C′分别与直线BC相交于P、Q.
(1)四边形的形状是 ,
当α=90°时,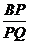 的值是
.
的值是
.
(2)①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求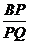 的值;
的值;
②如图3,当四边形OA′B′C′的顶点B′落在直线BC上时,求ΔOPB′的面积.
(3)在四边形OABC旋转过程中,当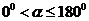 时,是否存在这样的点P和点Q,使BP=
时,是否存在这样的点P和点Q,使BP=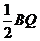 ?若存在,请直接写出点P的坐标;基不存在,请说明理由.
?若存在,请直接写出点P的坐标;基不存在,请说明理由.
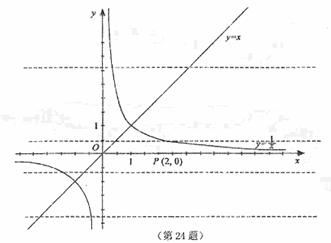
037]已知平行于x轴的直线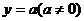 与函数
与函数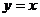 和函数
和函数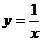 的图像分别交于点A和点B,又有定点P(2,0) .
的图像分别交于点A和点B,又有定点P(2,0) .
(1)若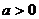 ,且tan∠POB=
,且tan∠POB=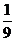 ,求线段AB的长;
,求线段AB的长;
(2)在过A,B两点且顶点在直线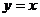 上的抛物线中,已知线段AB=
上的抛物线中,已知线段AB=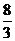 ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
(3)已知经过A,B,P三点的抛物线,平移后能得到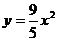 的图像,求点P到直线AB的距离。
的图像,求点P到直线AB的距离。
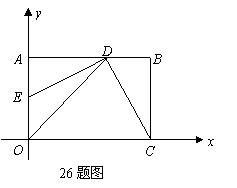
036]已知:如图,在平面直角坐标系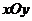 中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
(1)求过点E、D、C的抛物线的解析式;
(2)将∠EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为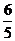 ,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;
(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
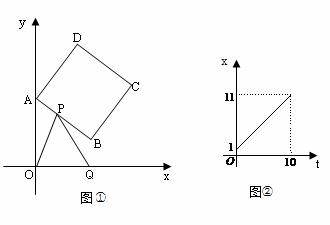
035]如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标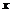 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相
等,若能,写出所有符合条件的t的值;若不能,请说明理由.
034]若P为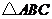 所在平面上一点,且
所在平面上一点,且 ,则点
,则点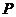 叫做
叫做 的费马点.
的费马点.
(1)若点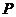 为锐角
为锐角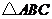 的费马点,且
的费马点,且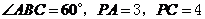 ,则
,则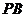 的值为________;
的值为________;
(2)如图,在锐角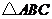 外侧作等边
外侧作等边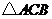 ′连结
′连结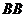 ′.
′.
求证: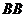 ′过
′过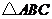 的费马点
的费马点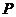 ,且
,且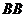 ′=
′=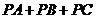 .
.

033]已知抛物线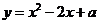 (
(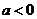 )与
)与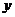 轴相交于点
轴相交于点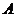 ,顶点为
,顶点为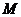 .直线
.直线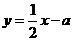 分别与
分别与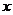 轴,
轴,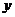 轴相交于
轴相交于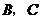 两点,并且与直线
两点,并且与直线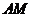 相交于点
相交于点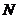 .
.
(1)填空:试用含 的代数式分别表示点
的代数式分别表示点 与
与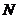 的坐标,则
的坐标,则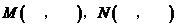 ;
;
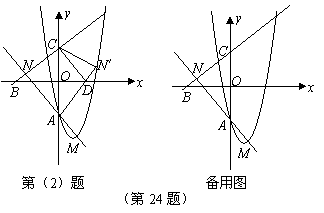
(2)如图,将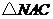 沿
沿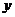 轴翻折,若点
轴翻折,若点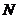 的对应点
的对应点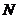 ′恰好落在抛物线上,
′恰好落在抛物线上,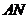 ′与
′与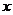 轴交于点
轴交于点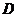 ,连结
,连结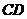 ,求
,求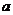 的值和四边形
的值和四边形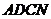 的面积;
的面积;
(3)在抛物线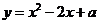 (
(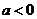 )上是否存在一点
)上是否存在一点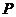 ,使得以
,使得以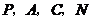 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出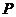 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
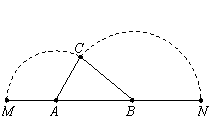
032]如图,已知A、B是线段MN上的两点,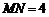 ,
,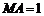 ,
,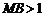 .以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设
.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设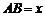 .
.
(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com