
1.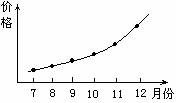 右边函数图像描述的是某商品在半年中的价格走势,
右边函数图像描述的是某商品在半年中的价格走势,
下列对该图理解正确的是
A.该商品很可能处于买方市场B.该商品的市场需求量迅速下降C.生产者会扩大该商品的生产规模
D.该商品的替代商品需求量会有所减少
财政部、商务部、工业和信息化部决定,自2009年2月1日起,在全国花4年时间全面推广“家电下乡”工程。对农民购买纳入补贴范围的家电产品给予一定比例(13%)的财政补贴。回答2-3题。
7. 如图,以A1、A2为焦 点的双曲线E与半径为c的圆O相交于C、D、C1、D1,连接CC1与OB交于点H,且有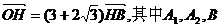 是圆O与坐标轴的交点,c为双曲线的半焦距.
是圆O与坐标轴的交点,c为双曲线的半焦距.
(1)当c=1时,求双曲线E的方程;
(2)试证:对任意正实数c,双曲线E的离心率为常数;
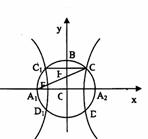 (3)连接A1C,与双曲线E交于点F,是否存在实数
(3)连接A1C,与双曲线E交于点F,是否存在实数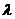 ,使
,使 恒成立?若存在,试求出
恒成立?若存在,试求出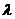 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
6. 如图, 已知线段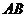 在直线
在直线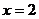 上移动,
上移动, 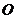 为原点.
为原点. 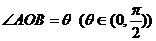 ,
动点
,
动点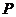 满足
满足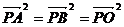 .
.
(Ⅰ) 求动点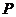 的轨迹方程;
的轨迹方程;
(Ⅱ) 当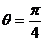 时, 动点
时, 动点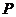 的轨迹与直线
的轨迹与直线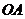 交于
交于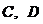 两点(点
两点(点 在点
在点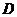 的下方), 且
的下方), 且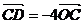 ,
求直线
,
求直线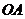 的方程.
的方程.
5. 在直角坐标系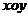 中,射线
中,射线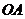 在第一象限且与
在第一象限且与 轴的正方向成定角
轴的正方向成定角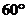 ,若点
,若点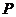 在射线
在射线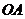 上运动,点
上运动,点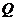 在
在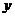 轴负半轴上运动,且
轴负半轴上运动,且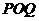 面积为定值
面积为定值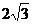 。
。
(1)求线段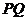 中点
中点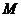 的轨迹
的轨迹 的方程;
的方程;
(2)若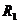 、
、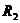 表示曲线
表示曲线 上的两个动点,且
上的两个动点,且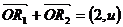 ,求
,求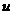 的最大值。
的最大值。
4. 已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为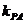 和
和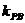 ,且满足
,且满足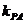 ·
·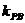 =t
(t≠0且t≠-1).
=t
(t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,
求t的取值范围.
3. 设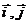 分别为直角坐标平面内x,y轴正方向的单位向量,若向量
分别为直角坐标平面内x,y轴正方向的单位向量,若向量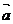 =
=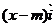 +
+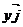 ,
,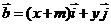 ,且 |
,且 |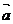 |+|
|+|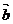 |=6,0<m<3,x>0,y
|=6,0<m<3,x>0,y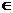 R。
R。
(1)求动点P (x,y)的轨迹方程;
(2)已知点A(-1,0),设直线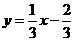 与点P的轨迹交于B,C两点,问是否存在实数m使得
与点P的轨迹交于B,C两点,问是否存在实数m使得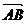
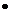
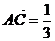 ?若存在,求出m的值;若不存在,试说明理由。
?若存在,求出m的值;若不存在,试说明理由。
2. 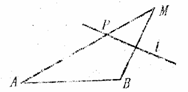 如图,A、B为两个定点,且 | AB |
=2
如图,A、B为两个定点,且 | AB |
=2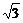 ,动点M到A的距离为4,线段MB的垂直平分线l交MA于点P,请你建立适当的直角坐标系.
,动点M到A的距离为4,线段MB的垂直平分线l交MA于点P,请你建立适当的直角坐标系.
(1)求点P的轨迹C的方程;
(2)设直线x-y+1=0与曲线C交于E、F两点,O为坐标原点,试求△OEF的面积.
1. 已知平面上一定点C(4,0)和一定直线l:x=1,P为该平面上一动点,作PQ⊥l于点Q,且(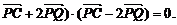
(Ⅰ)问点P在什么曲线上?并求出该曲线的方程;
(Ⅱ)设直线l:y=kx+1与(Ⅰ)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值;若不存在,说明理由.
24.设函数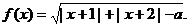
(1)当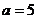 时,求函数
时,求函数 的定义域;
的定义域;
(2)若函数 的定义域为R,试求
的定义域为R,试求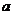 的取值范围。
的取值范围。
23.已知曲线C的极坐标方程是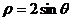 ,设直线
,设直线 的参数方程是
的参数方程是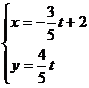 (
(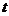 为参数)。
为参数)。
(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线 与
与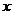 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
(本小题满分10分)
选修4-5:不等式选讲
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com