
4.函数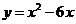 的减区间是( )
的减区间是( )
A.(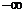 ,2] B.[2,
,2] B.[2, 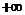 )
C.[3,
)
C.[3, 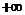 )
D.(
)
D.(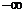 ,3]
,3]
3.已知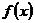 是偶函数,且
是偶函数,且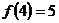 ,那么
,那么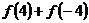 的值为
( )
的值为
( )
A.5
B.10
C.8
D.不确定
2.设集合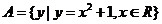 ,
, 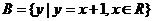 ,则
,则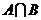 =( )
=( )
A 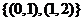 B
B 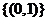 C
C 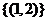 D
D 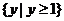

1.已知全集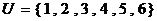 ,集合
,集合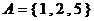 ,集合
,集合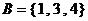 ,则
,则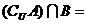 ( )
( )
A.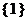 B.
B.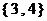 C.
C.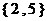 D.
D.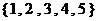

2.预习提纲:
(1)什么是等比数列?(2)等比数列的通项公式?(3)等比数列的通项公式的推导过程及推导思路?
●板书设计
|
课 题 例1 复习回顾 an=a1+(n-1)d 例2 公式Sn= 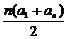 例3 =na1+ 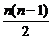 d d |
6.一个等差数列前4项的和是24,前5项的和与前2项的和的差是27,求这个等差数列的通项公式.
分析:将已知条件转化为数学语言,然后再解.
解:根据题意,得S4=24,S5-S2=27
则设等差数列首项为a1,公差为d,
即: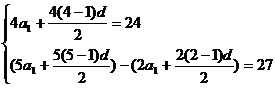
解之得: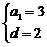 ∴am=3+2(n-1)=2n+1.
∴am=3+2(n-1)=2n+1.
Ⅳ.课时小结
通过本节学习,要能灵活应用等差数列的通项公式和前n项和公式解决一些相关问题.另外,需注意一重要结论:若一数列为等差数列,则Sk,S2k-Sk,S3k-S2k也成等差数列.
Ⅴ.课后作业
5.在小于100的正整数中共有多少个数能被3除余2?这些数的和是多少?
分析:满足条件的数属于集合,M={m|m=3n+2,m<100,m∈N*}
解:分析题意可得满足条件的数属于集合,M={m|m=3n+2,m<100,n∈N*}
由3n+2<100,得n<32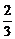 ,且m∈N*,∴n可取0,1,2,3,…,32.
,且m∈N*,∴n可取0,1,2,3,…,32.
即:在小于100的正整数中共有33个数能被3除余2.
把这些数从小到大排列出来就是:2,5,8,…,98.
它们可组成一个以a1=2,d=3,a33=98,n=33的等差数列.
由Sn=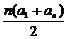 ,得S33=
,得S33=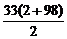 =1650.
=1650.
答案:在小于100的正整数中共有33个数能被3除余2,这些数的和是1650.
提高学生的应用意识.
●教学重点
熟练掌握等差数列的求和公式.
●教学难点
灵活应用求和公式解决问题.
●教学方法
讲练结合法
结合具体例子讲解分析问题,解决问题的方法,从而提高学生分析问题,解决问题的能力.
●教具准备
投影片两张
第一张:
[例1]求集合M={m|m=7n,n∈N*,且m<100}的元素个数,并求这些元素的和.
[例2]已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
第二张:
[例3]已知数列{an}是等差数列,Sn是其前n项和.
求证:S6,S12-S6,S18-S12成等差数列,设其k∈N*,Sk,S2k-Sk,S3k-S2k成等差数列吗?
●教学过程
Ⅰ.复习回顾
[师]请同学们回顾一下等差数列的通项公式及前n项和公式.
[生]通项公式:an=a1+(n-1)d,求和公式:Sn=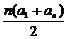 =na1+
=na1+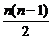 d
d
Ⅱ.讲授新课
(打出投影片
下面结合这些例子,来看如何应用上述知识解决一些相关问题.
[例1]分析:满足条件的n的取值个数即为集合M的元素个数,这些元素若按从小到大排列,则是一等差数列.
解:由m<100,得7n<100,即n<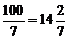
所以满足上面不等式的正整数n共有14个,即集合M中的元素共有14个,将它们从小到大可列出,得:7,7×2,7×3,7×4,…7×14,即:7,14,21,28,…98
这个数列是等差数列,记为{an},其中a1=7,a14=98,n=14
则S14=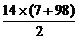 =735
=735
答:集合M中共有14个元素,它们和等于735.
这一例题表明,在小于100的正整数中共有14个数是7的倍数,它们的和是735.
[例2]分析:将已知条件代入等差数列前n项和的公式后,可得到两个关于a1与d的关系,然后确定a1与d,从而得到所求前n项和的公式.
解:由题意知S10=310,S20=1220,
将它们代入公式Sn=na1+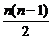 d,得到
d,得到
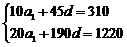
解这个关于a1与d的方程组,得到a1=4,d=6
所以Sn=4n+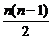 ×6=3n2+n
×6=3n2+n
这就是说,已知S10与S20,可以确定这个数列的前n项和的公式,这个公式是Sn=3n2+n.
下面,同学们再来思考这样一个问题:(打出投影片§3.3.2 B)
[生]仔细分析题意,解决问题.
解:设{an}的首项是a1,公差为d,则S3=a1+a2+a3
S6-S3=a4+a5+a6=(a1+3d)+(a2+3d)+(a3+3d)=(a1+a2+a3)+9d=S3+9d
S9-S6=a7+a8+a9=(a4+3d)+(a5+3d)+(a6+3d)=(a4+a5+a6)+9d=(S6-S3)+9d
∴S3,S6-S3,S9-S6成等差数列.
同理可得Sk,S2k-Sk,S3k-S2k成等差数列.
[Sk=a1+a2+…+ak(S2k-Sk)=ak+1+ak+2+…+a2k=(a1+kd)+(a2+kd)+…+(ak+kd)=(a1+a2+…+ak)+k2d=Sk+k2d
(S3k-S2k)=a2k+1+a2k+2+…+a3k=(ak+1+kd)+(ak+2+kd)+…+(a2k+kd)=(ak+1+ak+2+…+a2k)+k2d=(S2k-Sk)+k2d
∴Sk,S2k-Sk,S3k-S2k是以Sk为首项,k2d为公差的等差数列.]
Ⅲ.课堂练习
[生](板演)课本
4.求集合M={m|m=2n-1,n∈N*,且m<60}的元素个数,并求这些元素的和.
解:由2n-1<60,得n<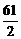 ,又∵n∈N*
,又∵n∈N*
∴满足不等式n<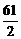 的正整数一共有30个.
的正整数一共有30个.
即:集合M中一共有30个元素,可列为:1,3,5,7,9,…,59,组成一个以a1=1,a30=59,n=30的等差数列.
∵Sn=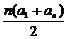 ,∴S30=
,∴S30=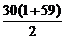 =900.
=900.
答案:集合M中一共有30个元素,其和为900.
评述:要注意看清所有的条件.
2.了解等差数列的一些性质,并会用它们解决一些相关问题.
1.进一步熟练掌握等差数列的通项公式和前n项和公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com