
7、(2009福建厦门一中)设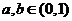 ,则关于
,则关于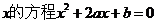 在
在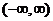 上有
上有
两个不同的零点的概率为______________
答案 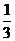
6、(2009广东中山市一模)若数据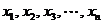 的平均数
的平均数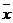 =5,方差
=5,方差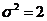 ,则数据
,则数据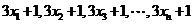 的平均数为 ,方差为 .
的平均数为 ,方差为 .
答案
5、(2009和平区一模)在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于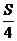 的概率是 ( )
的概率是 ( )
(A)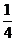 (B)
(B) (C)
(C) (D)
(D)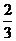
答案 C
4、(2009宁波十校联考)将一枚骰子抛掷两次,若先后出现的点数分别为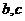 ,则方程
,则方程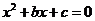 有实根的概率为 ( )
有实根的概率为 ( )
A 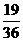 B
B
 C
C
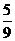 D
D
答案 A
3、(湖北省武汉二中2009届高三3月测试题)某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数为
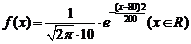 ,则下列命题中不正确的是 ( )
,则下列命题中不正确的是 ( )
A. 该市这次考试的数学平均成绩为80分
B. 分数在120分以上的人数与分数在60分以下的人数相同
C. 分数在110分以上的人数与分数在50分以下的人数相同
D. 该市这次考试的数学成绩标准差为10
答案 B
2、(2009广东江门市模拟)如图1,分别以正方形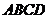 的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在阴影区域的概率为 ( )
的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在阴影区域的概率为 ( )
 A.
A.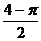 B.
B.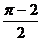 C.
C.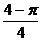 D.
D.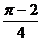
答案
1、(2009年山东省乐陵一中高三模拟)一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是 ( )
A.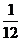 B.
B.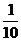 C.
C.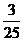 D.
D.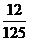
答案 D
2009年联考题
17、(2006年全国Ⅱ理18)某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.
解(1.) 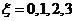
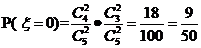
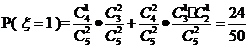
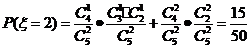
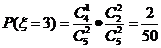
所以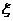 的分布列为
的分布列为
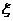 |
0 |
1 |
2 |
3 |
|
P |
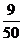 |
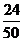 |
 |
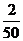 |
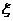 的数学期望E(
的数学期望E(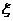 )=
)=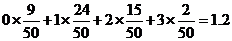
(2)P(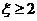 )=
)=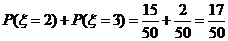
16、(2006北京卷)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9.
(Ⅰ) 应聘者用方案一考试通过的概率
p1=P(A·B·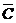 )+P(
)+P(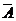 ·B·C)+P(A·
·B·C)+P(A·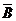 ·C)+P(A·B·C)
·C)+P(A·B·C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.03+0.27+0.18+0.27=0.75.
(Ⅱ) 应聘者用方案二考试通过的概率
p2=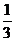 P(A·B)+
P(A·B)+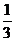 P(B·C)+
P(B·C)+ 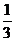 P(A·C)
P(A·C)
=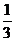 ×(0.5×0.6+0.6×0.9+0.5×0.9)=
×(0.5×0.6+0.6×0.9+0.5×0.9)=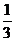 ×1.29=0.43
×1.29=0.43
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com