
6、(09海南23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C :
: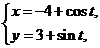 (t为参数), C
(t为参数), C :
: (
(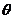 为参数)。
为参数)。
(1)化C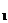 ,C
,C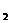 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C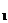 上的点P对应的参数为
上的点P对应的参数为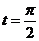 ,Q为C
,Q为C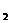 上的动点,求
上的动点,求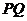 中点
中点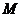 到直线
到直线
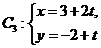 (t为参数)距离的最小值。
(t为参数)距离的最小值。
解:(Ⅰ)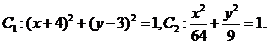
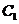 为圆心是(
为圆心是(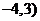 ,半径是1的圆.
,半径是1的圆.
 为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当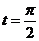 时,
时,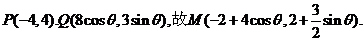
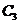 为直线
为直线
从而当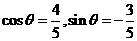 时,
时,
5、(09海南22)本小题满分10分)选修4-1:几何证明选讲
如图,已知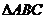 的两条角平分线
的两条角平分线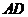 和
和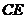 相交于H,
相交于H,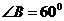 ,F在
,F在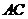 上,
上,
且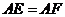 。
。
(Ⅰ)证明:B,D,H,E四点共圆:
(Ⅱ)证明: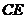 平分
平分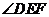 。
。
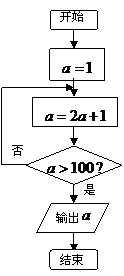 解:(Ⅰ)在△ABC中,因为∠B=60°,
解:(Ⅰ)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°. 

于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆.
(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由(Ⅰ)知B,D,H,E四点共圆,
所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,由已知可得EF⊥AD,
可得∠CEF=30°.
所以CE平分∠DEF.
4、(09安徽理12)以直角坐标系的原点为极点,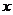 轴的正半轴为极轴,并在两种坐标系中
轴的正半轴为极轴,并在两种坐标系中
取相同的长度单位。已知直线的极坐标方程为 ,它与曲线
,它与曲线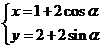
(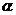 为参数)相交于两点A和B,则|AB|=_______.
为参数)相交于两点A和B,则|AB|=_______.
[解析]直线的普通方程为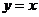 ,曲线的普通方程
,曲线的普通方程
∴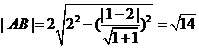
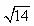 答案
答案
3、(天津理13) 设直线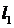 的参数方程为
的参数方程为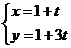 (t为参数),直线
(t为参数),直线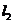 的方程为y=3x+4则
的方程为y=3x+4则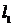 与
与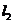 的距离为_______
的距离为_______
[解析]由题直线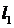 的普通方程为
的普通方程为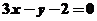 ,故它与与
,故它与与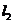 的距离为
的距离为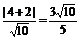 。
。
答案 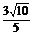
2、(09广东理15) (几何证明选讲选做题)如图3,点A、B、C是圆O上的点,且AB=4,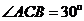 ,则圆O的面积等于 .
,则圆O的面积等于 . 

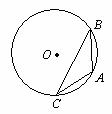
图3
[解析]连结AO,OB,因为 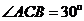 ,所以
,所以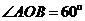 ,
,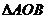 为等边三角形,故圆
为等边三角形,故圆
O的半径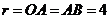 ,圆O的面积
,圆O的面积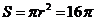 .
.
答案
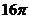
1、(09广东理14)(坐标系与参数方程选做题)若直线 (t为参数)与直线
(t为参数)与直线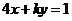 垂直,则常数
垂直,则常数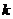 = .
= .
[解析]将 化为普通方程为
化为普通方程为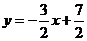 ,斜率
,斜率 ,
,
当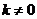 时,直线
时,直线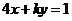 的斜率
的斜率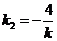 ,由
,由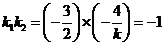 得
得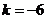 ;
;
当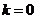 时,直线
时,直线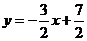 与直线
与直线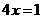 不垂直.
不垂直.
综上可知,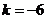 .
.
答案 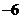
2009年高考题
6、(2007浦东新区高三二轮复习)某研究所试制出一大批特种陶瓷刀,他们从这批产品中随机抽取了50个样本,检测它们的硬度和耐磨度.硬度和耐磨度各分为5个档次,检测结果如下表.如表中所示硬度为5、耐磨度为4的刀具有3把.若在该批产品中任选一把刀具,其硬度记为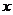 ,耐磨度记为
,耐磨度记为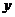 .
.
(1)试根据这50个样本估计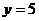 的概
的概
率是多少?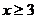 且
且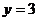 的概率是多少?
的概率是多少?
(2)若从这一大批产品中任 意取出3把
刀具,则这3把刀具至少有2把的耐磨度
为5的概率是多少?
(3)根据这50个样本估计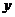 的期望值.
的期望值.
解:(1) 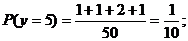
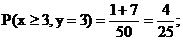
(2)由(1)可知,任取1把刀具,其耐磨度为5的概率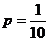 ,故任取3把,至少有2把耐磨度为5的概率为
,故任取3把,至少有2把耐磨度为5的概率为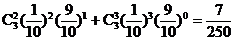 ;
;
(3)由题意可知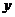 的分布列为
的分布列为
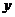 |
5 |
4 |
3 |
2 |
1 |
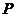 |
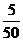 |
 |
 |
 |
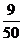 |
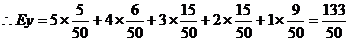 .
.
5、(2008年东北三省三校高三第一次联合模拟考试)
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号。若拿出球的标号是3的倍数,则得1分,否则得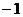 分。
分。
(1)求拿4次至少得2分的概率;
(2)求拿4次所得分数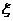 的分布列和数学期望。
的分布列和数学期望。
解(1)设拿出球的号码是3的倍数的为事件A,则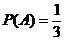 ,
,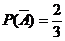 ,拿4次至少得2分包括2分和4分两种情况。
,拿4次至少得2分包括2分和4分两种情况。
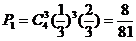 ,
,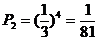 ,
,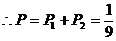
(2)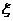 的可能取值为
的可能取值为 ,则
,则
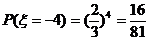 ;
;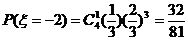 ;
;
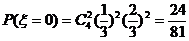 ;
;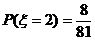 ;
;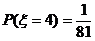 ;
;
 分布列为
分布列为
|
P |
-4 |
-2 |
0 |
2 |
4 |
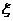 |
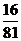 |
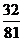 |
 |
 |
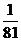 |
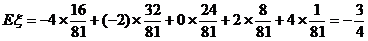
4、(2007石景山区高三二轮复习)一次单元测试由50个选择题构成,每个选择题有4个选项,其中恰有一个是正确的答案,每题选择正确得3分,不选或选错得0分,满分150分.学生甲选对任一题的概率为0.8,则该生在这次测试中成绩的期望值是_________,标准差是_____________.
答案 120 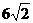
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com