
14.(2007四川)已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,u)(u,N +),其中为正实数.
(Ⅰ)用xx表示xn+1;
(Ⅱ)若a1=4,记an=lg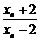 ,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
解析:本题综合考查数列、函数、不等式、导数应用等知识,以及推理论证、计算及解决问题的能力.
(Ⅰ)由题可得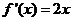 .
.
所以曲线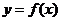 在点
在点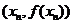 处的切线方程是:
处的切线方程是: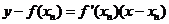 .
.
即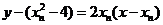 .
.
令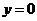 ,得
,得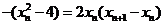 .
.
即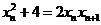 .
.
显然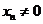 ,∴
,∴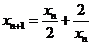 .
.
(Ⅱ)由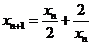 ,知
,知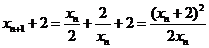 ,同理
,同理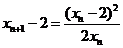 .
.
故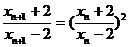 .
.
从而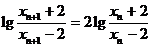 ,即
,即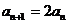 .所以,数列
.所以,数列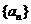 成等比数列.
成等比数列.
故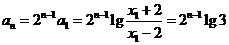 .
.
即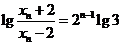 .
.
从而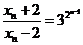
所以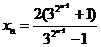
(Ⅲ)由(Ⅱ)知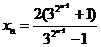 ,
,
∴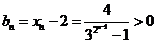
∴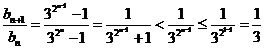
当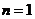 时,显然
时,显然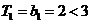 .
.
当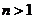 时,
时,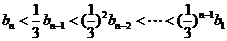
∴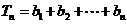
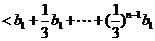
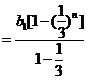
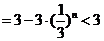 .
.
综上,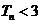
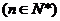 .
.
13.(2007浙江)已知数列{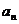 }中的相邻两项
}中的相邻两项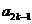 、
、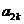 是关于x的方程
是关于x的方程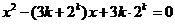 的两个根,且
的两个根,且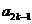 ≤
≤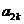 (k =1,2,3,…).
(k =1,2,3,…).
(I)求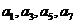 及
及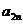 (n≥4)(不必证明);(Ⅱ)求数列{
(n≥4)(不必证明);(Ⅱ)求数列{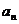 }的前2n项和S2n.
}的前2n项和S2n.
(I)解:方程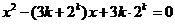 的两个根为
的两个根为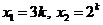 .
.
当k=1时,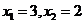 ,所以
,所以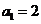 ;
;
当k=2时,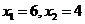 ,所以
,所以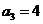 ;
;
当k=3时,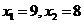 ,所以
,所以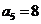 ;
;
当k=4时,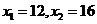 ,所以
,所以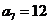 ;
;
因为n≥4时,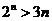 ,所以
,所以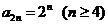
(Ⅱ)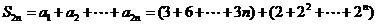 =
=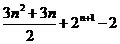 .
.
12.(2007湖南)已知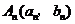 (
(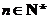 )是曲线
)是曲线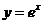 上的点,
上的点,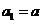 ,
, 是数列
是数列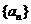 的前
的前 项和,且满足
项和,且满足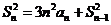 ,
,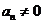 ,
,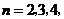 ….
….
(I)证明:数列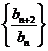 (
(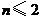 )是常数数列;
)是常数数列;
(II)确定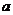 的取值集合
的取值集合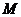 ,使
,使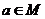 时,数列
时,数列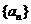 是单调递增数列;
是单调递增数列;
(III)证明:当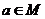 时,弦
时,弦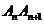 (
(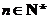 )的斜率随
)的斜率随 单调递增
单调递增
解:(I)当 时,由已知得
时,由已知得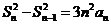 .
.
因为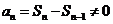 ,所以
,所以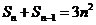 .
…… ①
.
…… ①
于是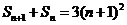 .
……②
.
……②
由②-①得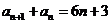 .
…… ③
.
…… ③
于是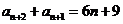 .
…… ④
.
…… ④
由④-③得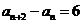 ,
…… ⑤
,
…… ⑤
所以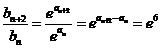 ,即数列
,即数列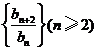 是常数数列.
是常数数列.
(II)由①有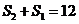 ,所以
,所以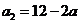 .由③有
.由③有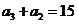 ,
,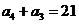 ,所以
,所以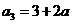 ,
,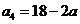 .
.
而 ⑤表明:数列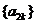 和
和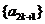 分别是以
分别是以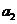 ,
,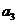 为首项,6为公差的等差数列,
为首项,6为公差的等差数列,
所以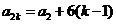 ,
,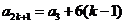 ,
,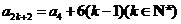 ,
,
数列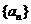 是单调递增数列
是单调递增数列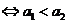 且
且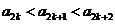 对任意的
对任意的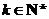 成立.
成立.
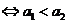 且
且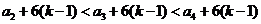
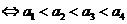
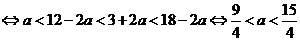 .
.
即所求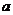 的取值集合是
的取值集合是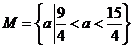 .
.
(III)解法一:弦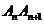 的斜率为
的斜率为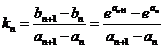
任取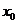 ,设函数
,设函数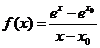 ,则
,则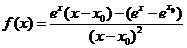
记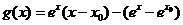 ,则
,则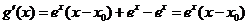 ,
,
当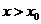 时,
时,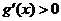 ,
,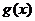 在
在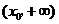 上为增函数,
上为增函数,
当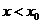 时,
时,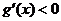 ,
,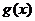 在
在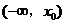 上为减函数,
上为减函数,
所以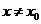 时,
时,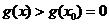 ,从而
,从而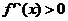 ,所以
,所以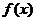 在
在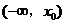 和
和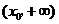 上都是增函数.
上都是增函数.
由(II)知,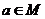 时,数列
时,数列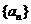 单调递增,
单调递增,
取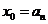 ,因为
,因为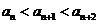 ,所以
,所以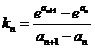
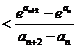 .
.
取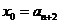 ,因为
,因为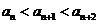 ,所以
,所以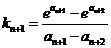
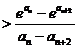 .
.
所以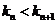 ,即弦
,即弦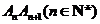 的斜率随
的斜率随 单调递增.
单调递增.
解法二:设函数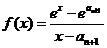 ,同解法一得,
,同解法一得,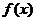 在
在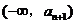 和
和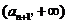 上都是增函数,
上都是增函数,
所以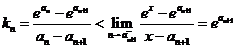 ,
,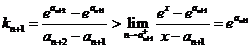 .
.
故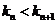 ,即弦
,即弦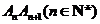 的斜率随
的斜率随 单调递增.
单调递增.
11.(2008山东卷)将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:
a1
a2 a3
a4 a5 a6
a7 a8 a9 a10
……
记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1. Sn为数列{bn}的前n项和,且满足=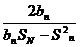 1=(n≥2).
1=(n≥2).
(Ⅰ)证明数列{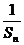 }成等差数列,并求数列{bn}的通项公式;
}成等差数列,并求数列{bn}的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当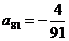 时,求上表中第k(k≥3)行所有项和的和.
时,求上表中第k(k≥3)行所有项和的和.
10.(2008全国I)设函数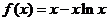 .数列
.数列 满足
满足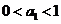 ,
,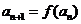 .
.
(Ⅰ)证明:函数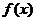 在区间
在区间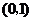 是增函数;
是增函数;
(Ⅱ)证明: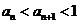 ;
;
(Ⅲ)设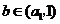 ,整数
,整数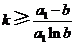 .证明:
.证明: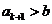 .
.
(Ⅰ)证明: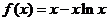 ,
,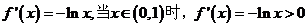
故函数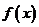 在区间(0,1)上是增函数;
在区间(0,1)上是增函数;
(Ⅱ)证明:(用数学归纳法)(i)当n=1时,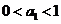 ,
,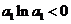 ,
,
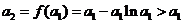
由函数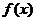 在区间
在区间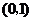 是增函数,且函数
是增函数,且函数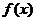 在
在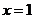 处连续,则
处连续,则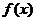 在区间
在区间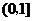 是增函数,
是增函数,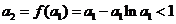 ,即
,即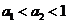 成立;
成立;
(ⅱ)假设当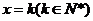 时,
时,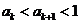 成立,即
成立,即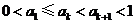
那么当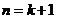 时,由
时,由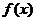 在区间
在区间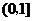 是增函数,
是增函数,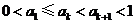 得
得
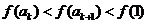 .而
.而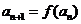 ,则
,则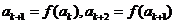 ,
,
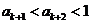 ,也就是说当
,也就是说当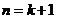 时,
时,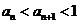 也成立;
也成立;
根据(ⅰ)、(ⅱ)可得对任意的正整数 ,
,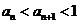 恒成立.
恒成立.
(Ⅲ)证明:由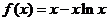 .
.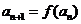 可
可
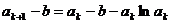
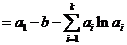
1, 若存在某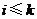 满足
满足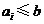 ,则由⑵知:
,则由⑵知: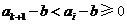
2, 若对任意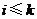 都有
都有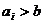 ,则
,则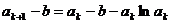
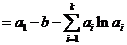
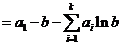
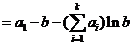
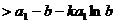
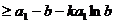
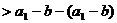
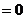 ,即
,即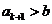 成立.
成立.
9.(2006广东卷)在德国不来梅举行的第48届世乒赛期间,某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品,其中第1堆只有1层,就一个球;第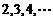 堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第
堆最底层(第一层)分别按图4所示方式固定摆放,从第二层开始,每层的小球自然垒放在下一层之上,第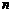 堆第
堆第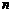 层就放一个乒乓球,以
层就放一个乒乓球,以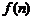 表示第
表示第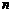 堆的乒乓球总数,则
堆的乒乓球总数,则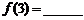 ;
;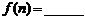 (答案用
(答案用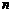 表示).
表示).
答案 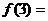 10,
10,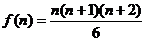
8.(2007重庆)设{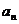 }为公比q>1的等比数列,若
}为公比q>1的等比数列,若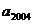 和
和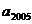 是方程
是方程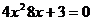 的两根,则
的两根,则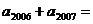 _____.
_____.
答案 18
7.(2008湖北)观察下列等式:
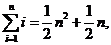
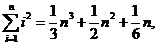
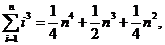
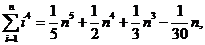
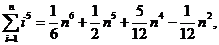
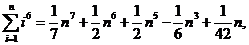
……………………………………
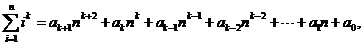
可以推测,当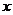 ≥2(
≥2(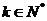 )时,
)时,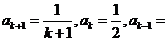
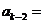 .
.
答案 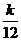 0
0
6.(2008江苏)将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
. . . . . . .
按照以上排列的规律,第n 行(n ≥3)从左向右的第3 个数为 .
答案 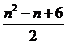
5.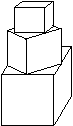 (2005重庆卷) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且改塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
(2005重庆卷) 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且改塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
A. 4 B.5.
C.6 D.7
答案 C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com