
2.(2009青岛一模)已知等差数列 的公差为
的公差为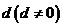 ,且
,且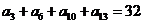 ,若
,若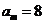 ,则
,则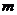 为
为
A.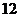 B.
B. 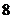 C.
C.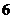 D.
D. 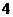
答案B
1.(2009临沂一模)在等差数列{an}中,若a2+a4+a6+a8+a10=80,则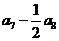 的值为
的值为
A、4 B、6 C、8 D、10
答案C
16.(2009闵行三中模拟)已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数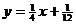 图像上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形。
图像上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形。
⑴求数列{yn}的通项公式,并证明{yn}是等差数列;
⑵证明xn+2-xn为常数,并求出数列{xn}的通项公式;
⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
解:(1)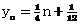 (nÎN),∵yn+1-yn=
(nÎN),∵yn+1-yn=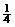 ,∴{yn}为等差数列 ………………4分
,∴{yn}为等差数列 ………………4分
(2)因为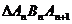 与
与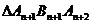 为等腰三角形.
为等腰三角形.
所以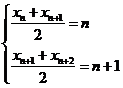 ,两式相减得
,两式相减得
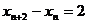 。………………7分
。………………7分
注:判断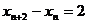 得2分,证明得1分
得2分,证明得1分
∴x1,x3,x5,…,x2n-1及x2,x4,x6 ,…,x2n都是公差为2的等差数列,………………6分
∴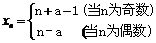 ………………10分
………………10分
(3)要使AnBnAn+1为直角三形,则 |AnAn+1|=2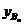 =2(
=2(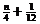 )Þxn+1-xn=2(
)Þxn+1-xn=2(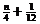 )
)
当n为奇数时,xn+1=n+1-a,xn=n+a-1,∴xn+1-xn=2(1-a).
Þ2(1-a)=2(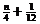 )
Þa=
)
Þa=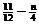 (n为奇数,0<a<1) (*)
(n为奇数,0<a<1) (*)
取n=1,得a=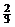 ,取n=3,得a=
,取n=3,得a=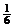 ,若n≥5,则(*)无解; ………………14分
,若n≥5,则(*)无解; ………………14分
当偶数时,xn+1=n+a,xn=n-a,∴xn+1-xn=2a.
∴2a=2(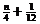 )Þa=
)Þa=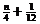 (n为偶数,0<a<1) (*¢),
(n为偶数,0<a<1) (*¢),
取n=2,得a=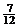 ,若n≥4,则(*¢)无解.
,若n≥4,则(*¢)无解.
综上可知,存在直角三形,此时a的值为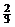 、
、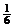 、
、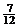 . ………………18分
. ………………18分

9月份更新
15.(2009聊城一模)过点P(1,0)作曲线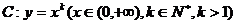 的切线,切点为M1,设M1在x轴上的投影是点P1。又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,…。依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为
的切线,切点为M1,设M1在x轴上的投影是点P1。又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,…。依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为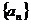 。
。
(1)求证数列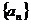 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;
(2)求证: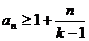 ;
;
(3)当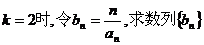 的前n项和Sn。
的前n项和Sn。
解:(1)对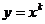 求导数,得
求导数,得 的切线方程是
的切线方程是
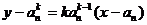
当n=1时,切线过点P(1,0),即0
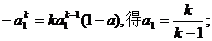
当n>1时,切线过点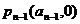 ,即0
,即0
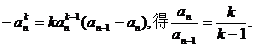
所以数列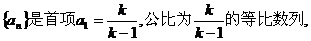
所以数列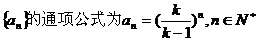
(2)应用二项公式定理,得
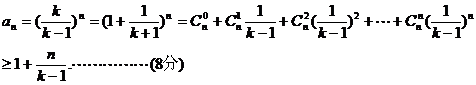
(3)当
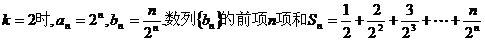 ,
,
同乘以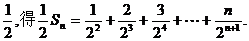
两式相减,得
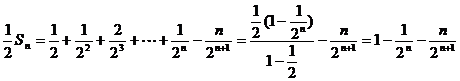
所以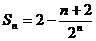
14.(2009韶关一模)已知函数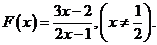
(I)求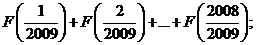
(II)已知数列 满足
满足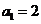 ,
,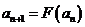 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ) 求证: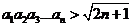 .
.
解:(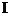 )因为
)因为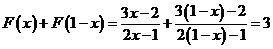
所以设S=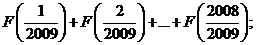
 (1)
(1)
S= ……….(2)
……….(2)
(1)+(2)得:
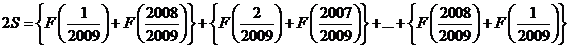 =
=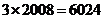 , 所以S=3012
, 所以S=3012
(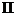 )由
)由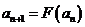 两边同减去1,得
两边同减去1,得
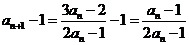
所以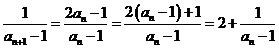 ,
,
所以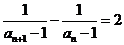 ,
,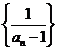 是以2为公差以
是以2为公差以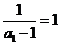 为首项的等差数列,
为首项的等差数列,
所以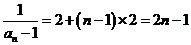
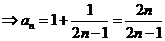
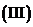 因为
因为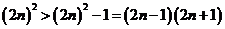
所以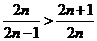
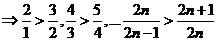
所以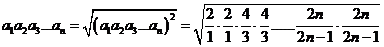
>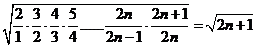
13.(2009龙岩一中第6次月考)某企业2008年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降.若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500(1+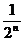 )万元(n为正整数).
)万元(n为正整数).
(Ⅰ)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元(须扣除技术改造资金),求An、Bn的表达式;
(Ⅱ)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
解: (Ⅰ)依题意知,数列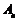 是一个以500为首项,-20为公差的等差数列,所以
是一个以500为首项,-20为公差的等差数列,所以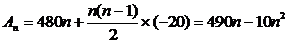 ,
,
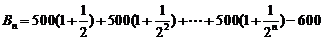 =
=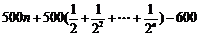
=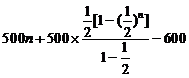 =
=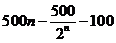
(Ⅱ)依题意得,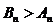 ,即
,即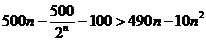 ,
,
可化简得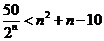 ,
,
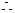 可设
可设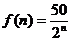 ,
,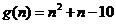
又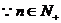 ,
,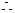 可设
可设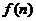 是减函数,
是减函数,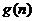 是增函数,又
是增函数,又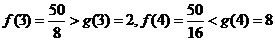
则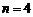 时不等式成立,即4年
时不等式成立,即4年
12.(辽宁省抚顺一中2009届高三数学上学期第一次月考)
已知方程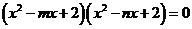 的四个根组成一个首项为
的四个根组成一个首项为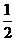 的等比数列,则|m-n|=
。
的等比数列,则|m-n|=
。
答案: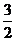 .
.
11.(2009江西师大附中)设等比数列{an}的前n项和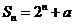 ,等差数列{bn}的前n项和
,等差数列{bn}的前n项和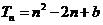 ,则a+b= .
,则a+b= .
答案 -1
10.(湖北省孝感市2009届高三3月统考理)
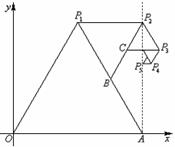 如图,以
如图,以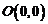 、
、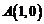 为顶点作正
为顶点作正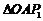 ,
,
再以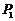 和
和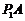 的中点
的中点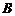 为顶点作正
为顶点作正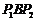 ,再
,再
以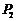 和
和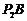 的中点
的中点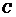 为顶点作正
为顶点作正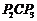 ,…,
,…,
如此继续下去。有如下结论:
①所作的正三角形的边长构成公比为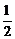 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线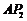 (
(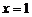 )上;
)上;
③第六个正三角形的不在第五个正三角形边上的顶点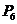 的坐标是
的坐标是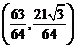 ;
;
④第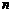 个正三角形的不在第
个正三角形的不在第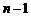 个正三角形边上的顶点
个正三角形边上的顶点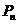 的横坐标是
的横坐标是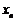 ,则
,则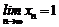 .
.
其中正确结论的序号是_____________.(把你认为正确结论的序号都填上)
答案 ①②③④
9.(2009广州一模)已知数列{an}的前n项和为Sn,对任意n∈N*
都有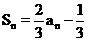 ,且1<Sk<9,则a1的值为______,k的的值为________.
,且1<Sk<9,则a1的值为______,k的的值为________.
答案 -1,4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com