
19.(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角
形,AB⊥平面BCD,AB=BC=a,E为BC的中点,
F在棱AC上,且AF=3FC.
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,
使MN∥平面DEF?若存在,说明点N的位置;若不
存在,试说明理由.
18.(本小题满分12分)
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评
分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定
有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道
题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:
(1)得60分的概率;
(2)得多少分的可能性最大?
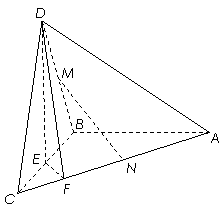
(3)所得分数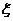 的数学期望(用分数表示,精确到0.01).
的数学期望(用分数表示,精确到0.01).
17.(本小题满分10分)
已知函数为偶函数,且其图象上相邻两对称轴之间的距离为.
(I)求函数的表达式。
(II)若,求的值.
16.已知椭圆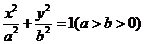 的左、右焦点分别为
的左、右焦点分别为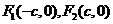 ,若椭圆上存在一点
,若椭圆上存在一点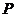 使
使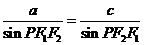 ,则该椭圆的离心率的取值范围为
.
,则该椭圆的离心率的取值范围为
.
15.已知函数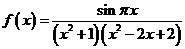 .
.
对于下列命题:
① 函数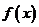 是周期函数;
是周期函数;
② 函数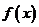 既有最大值又有最小值;
既有最大值又有最小值;
③ 函数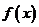 的定义域是R,且其图象有对称轴;
的定义域是R,且其图象有对称轴;
④ 对于任意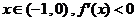 (
(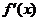 是函数
是函数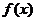 的导函数).
的导函数).
其中真命题的序号是 .(填写出所有真命题的序号)
14.已知A(-3,0),B(0,),O为坐标原点,点C在第二象限,且∠AOC=60°,
→=λ→+→,则实数λ的值是 .
13.已知等差数列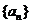 中,
中,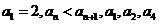 成等比数列,则
成等比数列,则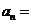 ______ _______.
______ _______.
12.已知双曲线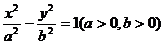 的左右焦点分别为F1,F2,点P在双曲线右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为 ( )
的左右焦点分别为F1,F2,点P在双曲线右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为 ( )
A.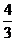 B.
B.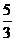 C.2
D.
C.2
D.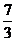
11.将4个相同的白球和5个相同的黑球全部放入3个不同的盒子中,每个盒子既要有白球,
又要有黑球,且每个盒子中球数不能少于2个,则所有不同的放法的种数为( )
A.12 B.3 C.18 D.6
10.已知棱长为3的正方体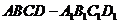 ,长为2的线段
,长为2的线段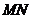 的一个端点
的一个端点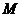 在
在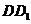 上
上
运动,另一个端点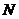 在底面
在底面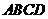 上运动.则线段
上运动.则线段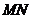 中点
中点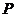 的轨迹与正方体的表面所
的轨迹与正方体的表面所
围成的较小的几何体的体积为( )
A.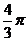 B.
B.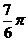 C.
C.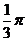 D.
D.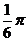
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com