
8.一个机器人从数轴上的原点出发,沿数轴方向,以每前进4步后退3步的程序运动,设该机器人每秒前进或后退1步,并且每步的距离为一个单位长度, 表示第
表示第 秒机器人在数轴上的位置所对应的数(如
秒机器人在数轴上的位置所对应的数(如 ),则
),则 。
。
7.连续两次掷骰子得到的点数依次为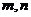 ,则以点
,则以点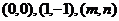 为顶点能构成直角三角形的概率是
。
为顶点能构成直角三角形的概率是
。
6.过点 引圆
引圆 的两条切线,则这两条切线与
的两条切线,则这两条切线与 轴,
轴,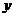 轴所围成的四边形的面积是
。
轴所围成的四边形的面积是
。
5.若函数 的导函数
的导函数 ,则函数
,则函数 的单调减区间是
。
的单调减区间是
。
4.设关于 的不等式:
的不等式: 的解集中整数的个数为
的解集中整数的个数为 ,数列
,数列 的前
的前 项的和为
项的和为 ,则
,则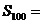 。
。
3.已知函数 的值域为
的值域为 ,则函数
,则函数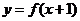 的值域是
。
的值域是
。
2.已知方程: 为纯虚数)有一实根。则
为纯虚数)有一实根。则 的值为
。
的值为
。
1.命题: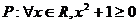 ,则
,则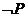 :
。
:
。
20.(本小题主要考查函数、导数、方程等知识,考查数形结合、化归与转化、分类与讨论的数学思想方法,以及运算求解能力)
(1)解:∵ ,∴
,∴ .
.
∵ 在
在 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,
∴当 时,
时, 取到极小值,即
取到极小值,即 .
.
∴ .
.
(2)解:由(1)知,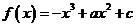 ,
,
∵1是函数 的一个零点,即
的一个零点,即 ,∴
,∴ .
.
∵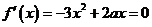 的两个根分别为
的两个根分别为 ,
,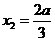 .
.
∵ 在
在 上是增函数,且函数
上是增函数,且函数 在
在 上有三个零点,
上有三个零点,
∴ ,即
,即 .
.
∴ .故
.故 的取值范围为
的取值范围为 .
.
(3)解:由(2)知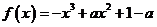 ,且
,且 .
.
要讨论直线 与函数
与函数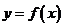 图像的交点个数情况,
图像的交点个数情况,
即求方程组 解的个数情况.
解的个数情况.
由 ,
,
得 .
.
即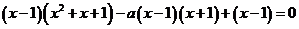 .
.
即 .
.
∴ 或
或 .
.
由方程 ,
(*)
,
(*)
得 .
.
∵ ,
,
若 ,即
,即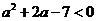 ,解得
,解得 .此时方程(*)无实数解.
.此时方程(*)无实数解.
若 ,即
,即 ,解得
,解得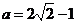 .此时方程(*)有一个实数解
.此时方程(*)有一个实数解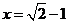 .
.
若 ,即
,即 ,解得
,解得 .此时方程(*)有两个实数解,分别为
.此时方程(*)有两个实数解,分别为 ,
, .
.
且当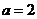 时,
时, ,
, .
.
综上所述,当 时,直线
时,直线 与函数
与函数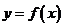 的图像有一个交点.
的图像有一个交点.
当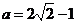 或
或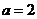 时,直线
时,直线 与函数
与函数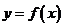 的图像有二个交点.
的图像有二个交点.
当 且
且 时,直线
时,直线 与函数
与函数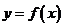 的图像有三个交点.
的图像有三个交点.
19.(本题满分16分)
(1)
 ,
, ……1分
……1分
∴当 时,
时,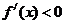 ,此时
,此时 单调递减
单调递减
当 时,
时, ,此时
,此时 单调递增 ……3分
单调递增 ……3分
∴ 的极小值为
的极小值为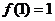 ……5分
……5分
(2)
 的极小值为1,即
的极小值为1,即 在
在 上的最小值为1,
上的最小值为1,
∴
 ,
,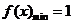 ……6分
……6分
令 ,
, , ……7分
, ……7分
当 时,
时, ,
,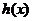 在
在 上单调递增 ……8分
上单调递增 ……8分
∴
∴在(1)的条件下, ……10分
……10分
(3)假设存在实数 ,使
,使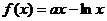 (
( )有最小值3,
)有最小值3,

①
当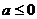 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),所以,此时
(舍去),所以,此时 无最小值. ……12分
无最小值. ……12分
②当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增
上单调递增
 ,
, ,满足条件. ……14分
,满足条件. ……14分
③ 当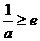 时,
时, 在
在 上单调递减,
上单调递减, ,
, (舍去),所以,此时
(舍去),所以,此时 无最小值.综上,存在实数
无最小值.综上,存在实数 ,使得当
,使得当 时
时 有最小值3
有最小值3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com