
13..现有下列命题:①命题“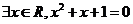 ”的否定是“
”的否定是“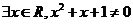 ”;② 若
”;② 若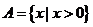 ,
,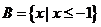 ,则
,则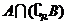 =
=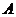 ;③函数
;③函数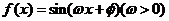 是偶函数的充要条件是
是偶函数的充要条件是 ;④若非零向量
;④若非零向量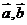 满足
满足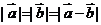 ,则
,则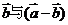 的夹角为 60º.其中正确命题的序号有________.(写出所有你认为真命题的序号)
的夹角为 60º.其中正确命题的序号有________.(写出所有你认为真命题的序号)
12.若复数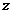 满足
满足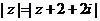 ,则
,则 的最小值是
的最小值是
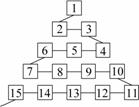
11.如图是从事网络工作者经常用来解释网络运作的蛇形模型:
数字1出现在第1行;数字2,3出现在第2行;数字6,5,
4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;
依此类推.则第99行从左至右算第67个数字为 4884 .
10.甲、乙、丙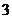 人站到共有
人站到共有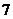 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站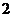 人,同一级台阶上的人不区分站的位置,则不同的站法种数是 (用数字作答).
人,同一级台阶上的人不区分站的位置,则不同的站法种数是 (用数字作答).
9.数列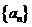 的构成法则如下:
的构成法则如下: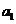 =1,如果
=1,如果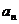
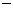 2为自然数且之前未出现过,则用递推公式
2为自然数且之前未出现过,则用递推公式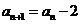 。否则用递推公式
。否则用递推公式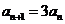 ,则
,则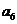 =
=
8.类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四体的下列的一些性质,①各棱长相等,同一顶点上的两条棱的夹角相等;②各个面都是全等的正三角形, 相邻两个面所成的二面角相等;③各个面都是全等的正三角形,同一顶点上的任何两条棱的夹角相等.你认为比较恰当的是 .
7.现安排5人去三个地区做志愿者,每个地区至少去1人,其中甲、乙不能去同一个地区,那么这样的安排方法共有 种(用数字作答)
答案:114 解析:第一步:对于甲、乙三个地区中挑选2个有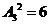 种方法;第二步:对于第三个地区有四种情况,第一是第三个地区放3人有1种可能;第二第三个地区放2人,另个一个地区放1人,则有6种可能第三是第三个地区放1人,另外一个地区放2人,则有6种可能;第四是第三个地区是放1人,然后另人二个地区也是1人有助6种可能;这样第二步共有19种情况;因此共有114种情况.
种方法;第二步:对于第三个地区有四种情况,第一是第三个地区放3人有1种可能;第二第三个地区放2人,另个一个地区放1人,则有6种可能第三是第三个地区放1人,另外一个地区放2人,则有6种可能;第四是第三个地区是放1人,然后另人二个地区也是1人有助6种可能;这样第二步共有19种情况;因此共有114种情况.
6.设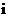 是虚数单位,则
是虚数单位,则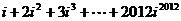 = .(用
= .(用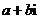 的形式表示,
的形式表示,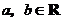 )
)
5.(08广东)命题“若函数f(x)=logxx(a>0,a≠1)在其定义域内是减函数,则logx2<0”的逆否命题是:
4.若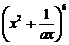 的二项展开式中
的二项展开式中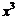 的系数为
的系数为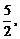 则
则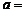 .(用数字作答)
.(用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com