
7. 将函数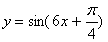 的图像上各点的横坐标伸长到原来的3倍,再向右平移
的图像上各点的横坐标伸长到原来的3倍,再向右平移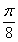 个单位,得到的函数的一个对称中心是( )
个单位,得到的函数的一个对称中心是( )
A.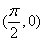
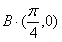 C.
C. 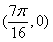 D.
D. 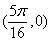
6.已知向量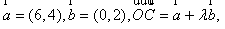 若点
若点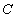 在函数
在函数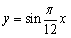 的图象上,则实数
的图象上,则实数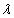 的值为( )
的值为( )
A.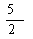 B.
B.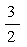 C.
C.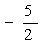 D.
D.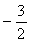
5. 已知函数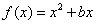 的图像在点
的图像在点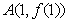 处切线的斜率为3,数列
处切线的斜率为3,数列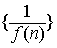 的前n项和为
的前n项和为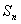 ,则
,则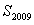 的值为( )
的值为( )
A.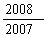 B.
B.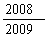 C.
C.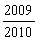 D.
D.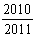
4. 已知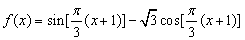 ,则
,则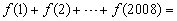 ( )
( )
A.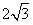 B.
B.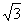 C.1
D.0
C.1
D.0
3. 函数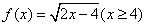 的反函数为( )
的反函数为( )
A.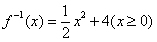 B.
B.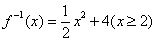
C.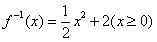 D.
D.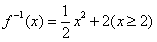
2. 若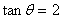 ,则
,则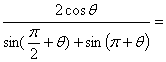 ( )
( )
A.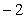 B.
B.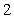 C.
C.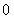 D.
D.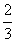
1. 集合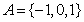 ,
,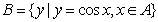 ,则
,则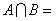 ( )
( )
A.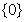 B.
B.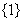 C.
C.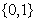 D.
D.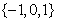
3、情感、态度和价值观
本课就象一面镜子,教师的责任就是把学生推到镜子面前让他们自己审视自己,通过这面镜子使学生学会自主选择的能力,自主制定自己的学习时间安排表。
[重点和难点]通过交流找到适合自己的学习方法。
[教学准备]多媒体辅助教学课件
[学生活动]小组讨论、填表
|
你的学习方式 |
|
|
任课老师的教学风格 |
|
|
你最喜欢的老师风格 |
|
|
你准备如何适应其他老师的教学方式 |
|
|
今后你将采用的学习方式 |
|
[课堂回声]有的同学也许会问,用什么方法学习最合适呢?这需要自己的探索。最重要的是自己认为用这种方法学习轻松、有趣,并且能达到满意的效果。你不妨试试不同的方法,但是不要用“死记硬背”这个方法。对于老师讲的方法,不要一点儿也不相信,也不能完全相信,可以试一试那种方法是否适合自己。希望大家用最适合自己的方法来学习知识,把握好这三年的学习生活。
[师生共勉]盛年不重来,一日难再晨。及时当勉励,岁月不待人。--陶渊明

第二课 把握学习新节奏--享受学习

教学目标:通过本节课的学习,让同学们认识学习、感受学习,从而领悟学习带来的快乐,能够喜欢学习。先从学生的学习感受出发让学生体会学习中的乐,进而让学生感受到享有学习权利本身就是一种快乐,从探索世界奥妙的角度进一步来激发学生的求知欲,体会学习的快乐。
教学重点:如何正确看待学习中的苦和乐,让同学们体会到享有学习的机会和权利本身就是一种快乐
教学难点:学习中苦与乐的关系
教学方法:调节教学、辩论、案例教学法等。
学习方法:合作探究、自学等
教学过程:
导入新课:我们经常会说要学会享受生活,享受生命,享受亲情等,因为生活、生命、亲情能够给我们带来心理的满足和快乐,那么学习也是一种享受吗?今天让我们来共同探讨一下吧。
学生活动(一):谈自己这几年在学习中的感受(提示:教师可以让学生根据自己小学时在学校的学习体会或参加各种辅导班的体会来谈,看看学习中有哪些乐趣,又有哪些困难和痛苦。)
师:世间的万事都是相对的,有好的一面自然有坏的一面,就如我们的学习生活,有苦涩夹杂也有快乐渗透。苦与乐是孪生姐妹--苦随乐,乐伴苦。学习生活是苦的,但其中的乐也不少,只要我们在艰苦的学习生活中寻找乐趣,那么我们的生活将更快乐,更充实。而且,同那些小小年纪就失去了上学的机会,就要为生活而忧愁的孩子相比,我们能够坐在明亮的教室里无忧无虑地学习是一件多么幸福的事。
图片:失学、失学的孩子、贫困地区的学童等(配合扩展资料使用)
为了保障青少年学习的机会和权利,国家也采取很多措施(略)
只有珍惜拥有的学习机会,才能学习更多的科学文化知识,才能不断地探索世界的奥妙。探索世界的奥妙,获得新知也是一种快乐.荀子曾说:“不登高山,不知天之高也;不临深溪,不知地之厚也。”的确,随着年龄的增长,随着知识的丰富,我们懂得了许多,却也发现我们不懂的更多。世界是如此奇妙,它以变幻莫测的姿态让我们感到新奇,也让我们感到困惑。
学生活动(二):小时候不能理解、现在已经理解的一个问题是什么?

你是怎样知道答案的?

学生活动(三):你还有哪些不知道的或不能理解的现象?
学生发言(略)
总结:当我们从学习中逐渐了解世界奥秘的时候,当我们的好奇心在学习中获得满足的时候,当我们通过学习发现自己潜能的时候,学习的快乐就洋溢在我们的心中。只要我们留心周围的世界,我们会发现生活中还有更多的有趣的现象和问题,需要我们不断地探索和发现。你知道以下奥秘吗?
恐龙是怎样灭绝的?
到底有没有外星人?
埃及金字塔是怎样建成的?
宇宙中存在黑洞吗?
总结:其实这些奥秘到今天为止,咱们人类还没有完成揭开。但是我们人类从来没有停止探索的脚步。例如,(出示我国“神舟”五号、探月计划、美国发射的火星探测车照片)为了探索更多的太空奥秘,我们研制的“神舟”五号载人飞般已经发射成功,探月计划已经启动,美国航天局发射的火星探测车已经在火星表面降落,这将帮人类揭开火星神秘的面纱迈进一大步。世界上还有许多现象我们无法解释,这带给我们的感觉是神秘、有趣,因此我们不断探索、发现、学习的过程也将会是快乐的过程,享受学习的过程,从无知走向有知的过程。希望同学们能够不断努力,好好把握初中三年的学习机会。































































3.空间图形是由点、线、面组成的
点、线、面的基本位置关系如下表所示:
|
图形 |
符号语言 |
文字语言(读法) |
 |
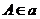 |
点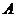 在直线 在直线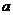 上 上 |
 |
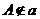 |
点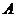 不在直线 不在直线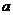 上 上 |
 |
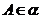 |
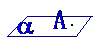
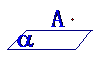
点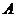 在平面 在平面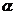 内 内 |
 |
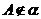 |
点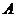 不在平面 不在平面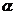 内 内 |
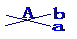 |
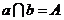 |
直线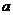 、 、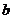 交于 交于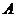 点 点 |
 |
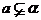 |
直线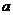 在平面 在平面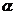 内 内 |
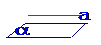 |
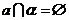 |
直线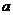 与平面 与平面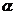 无公共点 无公共点 |
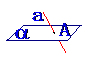 |
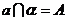 |
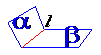
直线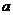 与平面 与平面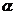 交于点 交于点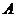 |
 |
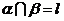 |
平面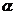 、 、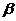 相交于直线 相交于直线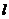 |
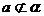 (平面
(平面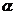 外的直线
外的直线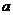 )表示
)表示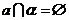 或
或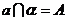

4平面的基本性质
公理1
如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内
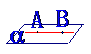 推理模式:
推理模式: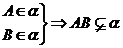 . 如图示:
. 如图示:
应用:是判定直线是否在平面内的依据,也可用于验证一个面是否是平面.
公理1说明了平面与曲面的本质区别.通过直线的“直”来刻划平面的“平”,通过直线的“无限延伸”来描述平面的“无限延展性”,它既是判断直线在平面内,又是检验平面的方法.
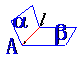 公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线
公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线
推理模式: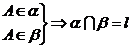 且
且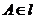 且
且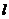 唯一如图示:
唯一如图示:

应用:①确定两相交平面的交线位置;②判定点在直线上
公理2揭示了两个平面相交的主要特征,是判定两平面相交的依据,提供了确定两个平面交线的方法.
公理3 经过不在同一条直线上的三点,有且只有一个平面
推理模式: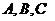 不共线
不共线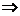 存在唯一的平面
存在唯一的平面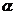 ,使得
,使得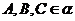

应用:①确定平面;②证明两个平面重合

“有且只有一个”的含义分两部分理解,“有”说明图形存在,但不唯一,“只有一个”说明图形如果有顶多只有一个,但不保证符合条件的图形存在,“有且只有一个”既保证了图形的存在性,又保证了图形的唯一性.在数学语言的叙述中,“确定一个”,“可以作且只能作一个”与“有且只有一个”是同义词,因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证.
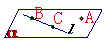 推论1
经过一条直线和直线外的一点有且只有一个平面
推论1
经过一条直线和直线外的一点有且只有一个平面
推理模式: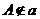
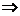 存在唯一的平面
存在唯一的平面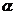 ,使得
,使得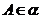 ,
,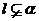

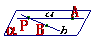 推论2
经过两条相交直线有且只有一个平面
推论2
经过两条相交直线有且只有一个平面
推理模式: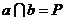
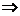 存在唯一的平面
存在唯一的平面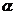 ,使得
,使得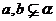

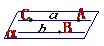 推论3 经过两条平行直线有且只有一个平面
推论3 经过两条平行直线有且只有一个平面
推理模式: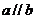
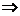 存在唯一的平面
存在唯一的平面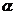 ,使得
,使得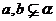

5平面图形与空间图形的概念:如果一个图形的所有点都在同一个平面内,则称这个图形为平面图形,否则称为空间图形
题型讲解

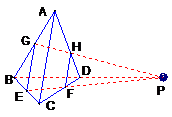
例1 如下图,四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=2∶3,DH∶HA=2∶3
求证:EF、GH、BD交于一点
分析:只要证明点E、F、G、H分别所在的直线EG和HF平行,由公理的推论3就可知它们共面在△ABD和△CBD中,由E、G分别是BC和AB的中点及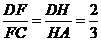 可得EG
可得EG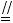
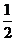 AC,HF
AC,HF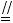
 AC,所以EG∥HF, 直线EF,GH是梯形的两腰,所以它们的延长线必相交于一点P,因此,要证三条直线EF、GH、BD交于一点,只要证点P在直线AC上即可
AC,所以EG∥HF, 直线EF,GH是梯形的两腰,所以它们的延长线必相交于一点P,因此,要证三条直线EF、GH、BD交于一点,只要证点P在直线AC上即可
事实上,由于BD是EF和GH分别所在平面ABC和平面ADC的交线,而点P是上述两平面的公共点,由公理2知P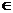 BD
BD
证法一:(几何法)连结GE、HF,
∵E、G分别为BC、AB的中点,
 ∴GE∥AC
∴GE∥AC
又∵DF∶FC=2∶3,DH∶HA=2∶3,
∴HF∥AC∴GE∥HF
故G、E、F、H四点共面
又∵EF与GH不能平行,
∴EF与GH相交,设交点为P
则P∈面ABD,P∈面BCD,而平面ABD∩平面BCD=BD
∴EF、GH、BD交于一点
证法二:(向量法)
由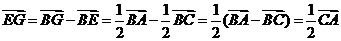

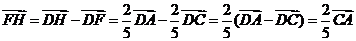

∴ 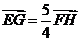 ,从而
,从而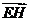 ∥
∥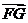

故G、E、F、H四点共面
又∵EF与GH不能平行,
∴EF与GH相交,设交点为P
则P∈面ABD,P∈面BCD,而平面ABD∩平面BCD=BD
∴EF、GH、BD交于一点
点评:证明线共点,常采用证两直线的交点在第三条直线上的方法,而第三条直线又往往是两平面的交线
例2 已知n条互相平行的直线l1,l2,l3…,ln分别与直线l相交于点A1,A2, …,An,求证:l1,l2,l3…,ln与l共面
…,An,求证:l1,l2,l3…,ln与l共面
分析:证明多条直线(三条或三条以上)共面,先由两条确定一个平面,再证其它直线在这个平面内,或者分别由两条直线确定几个平面,再证这些平面重合
证法一:因为l1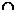 l=A1,所以l1与l确定平面α,设lk是与l1平行的直线中的任一条直线,且lk
l=A1,所以l1与l确定平面α,设lk是与l1平行的直线中的任一条直线,且lk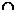 l=Ak,则
l=Ak,则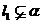 ,Ak
,Ak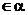 ,
,
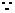 lk∥l1,设lk与l1确定平面
lk∥l1,设lk与l1确定平面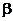 ,则
,则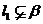 ,Ak
,Ak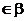 ,因此l1与Ak既在平面
,因此l1与Ak既在平面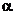 内又在平面
内又在平面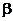 内,根据公理的推论1知过l1和其外一点的平面有且只有一个,所以
内,根据公理的推论1知过l1和其外一点的平面有且只有一个,所以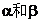 重合,从而由lk的任意性知l1,l2,l3…,ln共面
重合,从而由lk的任意性知l1,l2,l3…,ln共面
证法二: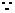 l1∥l2,l1∥l3
l1∥l2,l1∥l3 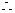 直线l1和l2及直线l1和l3分别确定一个平面
直线l1和l2及直线l1和l3分别确定一个平面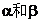
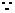 l1
l1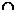 l=A1, l2
l=A1, l2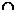 l=A2, l3
l=A2, l3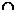 l=A3,
l=A3,
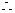 A1,A2
A1,A2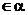 ,A2,A3
,A2,A3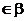 ,l
,l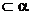 ,且l
,且l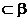 ,
,
α和β都是过相交直线l1和l的平面,而过两相交直线的平面有且只有一个
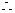 l1,l2,l3,l共面,同理可证l4,l5,…,ln都在由直线l1和l所确定的平面内
l1,l2,l3,l共面,同理可证l4,l5,…,ln都在由直线l1和l所确定的平面内
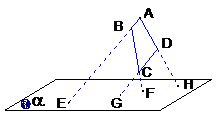
例3 如图,已知四边形ABCD中,AB∥CD,四条边AB,BC,DC,AD(或其延长线)分别与平面α相交于E,F,G,H四点,求证:四点E,F,G,H共线
证明: AB∥CD,
AB∥CD,
 AB,CD确定一个平面β,
AB,CD确定一个平面β,
 易知AB,BC,DC,AD都在β内,
易知AB,BC,DC,AD都在β内,
由平面的性质可知四点E,F,G,H都在β上,
因而,E,G,G,H必都在平面α与β的交线上,
所以四点E,F,G,H共线
例4 如图,在一封闭的正方体容器内装满水,M,N分别是AA1与C1D1的中点,由于某种原因,在D,M,N三点处各有一个小洞,为使此容器内存水最多,问应将此容器如何放置?此时水的上表面的形状怎样?
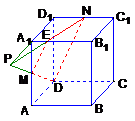 解:使过三点M,N,D的平面成为水平面时,容器内存水最多,至于水表面的形状,实质上就是过M,N,D三点所作正方体的截面的形状
解:使过三点M,N,D的平面成为水平面时,容器内存水最多,至于水表面的形状,实质上就是过M,N,D三点所作正方体的截面的形状
连结DM并延长DM交D1A1的延长线于P,
则点P既在截面内又在底面A1B1C1D1内,
连结PN交A1B1于E,连ME,ND,
则过M,N,D的截面就是四边形DMEN,
易证ME∥DN且ME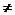 DN,因而它是一个梯形
DN,因而它是一个梯形
小结:
1证明“线共点”的方法,一般是先证两条直线相交于一点,然后再证其它的直线过这一点
2证明“线共面”的问题,一般先由公理3或推论确定一个平面,再证明其它的直线在这个平面内
3证明“点共线”的方法,一般都是通过证这些点在某两个平面的交线上来解决
4作几何体的截面图时,常利用平面的性质,设法确定所作截面上的关键点,从而确定截面图形
学生练习
1将命题“P∈l,Q∈l,且P∈α,Q∈α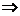 l
l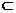 α”用文字语言表述是
α”用文字语言表述是
2若平面α∩平面β=直线l,点A∈α,A∈β则点 l ,其理由是
3下列命题中正确的是( )
A空间不同的三点确定一个平面
B空间两两相交的三条直线确定一个平面
C空间有三个角为直角的四边形一定是平面图形
D和同一条直线相交的三条平行直线一定在同一平面内
4一个水平放置的四边形的斜二测直观图是一底角为45°,腰和上底的长均为1的等腰梯形,那么原四边形的面积是( )
A2+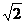 B1+
B1+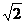 C
C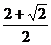 D
D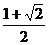
5E、F、G、H是三棱锥A-BCD的棱AB、AD、CD、CB上的点,延长EF、HG交于P点,则点P( )
A 一定在直线AC上 B 一定在直线BD上
C只在平BCD内 D只在平面ABD内
6空间三条直线中的一条直线与其它两条都相交,那么由这三条直线最多可确定平面的个数是( )个
A1 B 2 C 3 D4
7用一个平面截一个正方体,其截面是一个多边形,则这个多边形边数最多是( )
A 三 B四 C 六 D八
8 “直线上有一点在平面内”是“这条直线在这个平面内”的( )
A充分不必要条件 B必要不充分条件
C充要条件 D既不充分又不必要条件
9已知空间四点中无任何三点共线,那么这四点可以确定平面的个数是
10下列说法正确的是
1空间四边形的对角线一定不相交
2 四个角都是直角的四边形一定是平面图形
3两两相交的三条直线一定共面
4 在空间的四点,若无三点共线,则这四点一定不共面
11已知直线c和d与异面直线a,b都相交,则由直线c,d可确定的平面的个数为
12不重合的三个平面把空间分成n个部分(不包括平面本身)则n的可能值是
13已知不共面的三条直线a,b,c两两相交,求证:这三条直线交于一点
14已知A,B,C是空间不共线的三点,画直线AB,BC,CA设X,Y,Z分别表示直线BC,CA,AB上的任意一点,试问直线AX,BY,CZ是否共面?并证明你的结论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com