
22.[解析](Ⅰ)当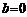 时,
时,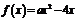 ,∴
,∴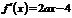 ,若
,若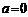 ,
,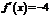 ,则在
,则在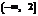 上,
上,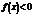 恒成立,符合题意;(3分)若
恒成立,符合题意;(3分)若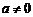 ,要使在
,要使在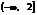 上
上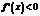 恒成立,即
恒成立,即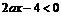 恒成立,也就是
恒成立,也就是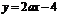 的图象在
的图象在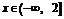 上总在
上总在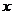 轴的下方,必须满足
轴的下方,必须满足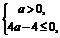 .∴
.∴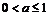 .综上所述,
.综上所述,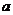 的取值范围是
的取值范围是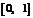 .(6分)(Ⅱ) 解法一:∵
.(6分)(Ⅱ) 解法一:∵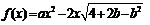 ,
,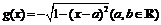 ,∴
,∴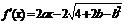 ,
,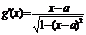 ,∵
,∵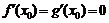 ,∴
,∴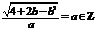 ,则
,则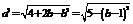 ,
,
∵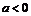 且
且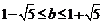 ,∴
,∴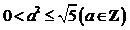 ,得
,得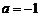 ,此时
,此时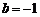 或
或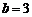 .
.
∴满足条件的整数对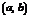 是
是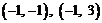 .…………(8分)
.…………(8分)
解法二:若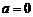 ,
,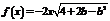 ,则
,则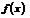 无最大值,故
无最大值,故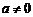 ,
,
∴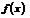 为二次函数,要使
为二次函数,要使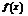 有最大值,必须满足
有最大值,必须满足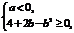 即
即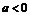 且
且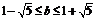 ,此时,
,此时,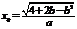 时,
时,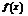 有最大值.…………(9分),
有最大值.…………(9分),
又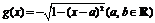 取最小值时,
取最小值时,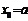 ,依题意,有
,依题意,有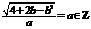 ,
,
则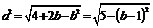 ,∵
,∵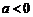 且
且
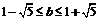 ,∴
,∴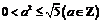 ,得
,得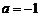 ,此时
,此时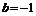 或
或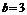 .
.
∴满足条件的整数对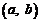 是
是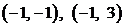 …………(12分)
…………(12分)
21.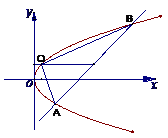 [解析](Ⅰ)解方程组
[解析](Ⅰ)解方程组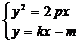 ,消去
,消去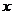 得
得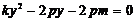 …①
…①
设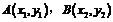 ,则
,则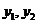 是方程①的两个根,∴
是方程①的两个根,∴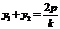 …②
…②
由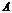 、
、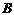 到
到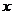 轴的距离之差为
轴的距离之差为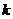 ,得
,得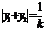 ③,由②、③解得
③,由②、③解得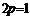 ,故
,故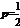 (6分)
(6分)
(Ⅱ)由(Ⅰ)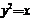 ,
,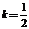 ,①式为
,①式为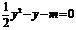 ,∴
,∴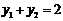 ,
,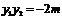
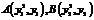 ,由题意点
,由题意点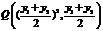 ,
,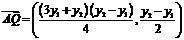 ,
,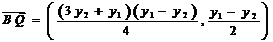 ,由
,由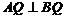 ,得
,得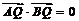 .
.
即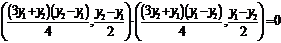 .由
.由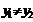 ,上式化简得
,上式化简得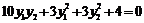 ,
,
即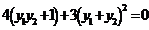 ,将
,将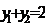 ,
,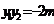 代入上式,有
代入上式,有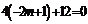 ,∴
,∴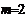 (12分)
(12分)
20.[解析](1)当n = 1时,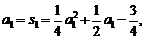 解出a1 = 3, …………(2分),
解出a1 = 3, …………(2分),
又4Sn = an2 +
2an-3 ①当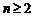 时,4sn-1 =
时,4sn-1 = 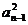 + 2an-1-3 ②
+ 2an-1-3 ②
①-②: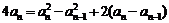 , 即
, 即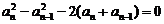 ,
,
∴ 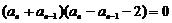 ,
,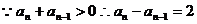 (
(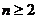 ),
),
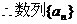 是以3为首项,2为公差的等差数列,
是以3为首项,2为公差的等差数列,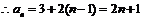 . (6分)
. (6分)
(2)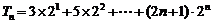 ③
③
又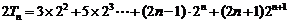 ④
④
④-③ 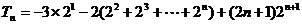
=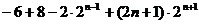
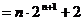 ……………12分
……………12分
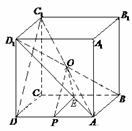
19.[解析]方法一:(Ⅰ)如图,连结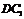 、
、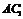 ∵
∵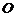 是正方体对角线
是正方体对角线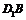 的中点,也是
的中点,也是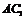 的中点,
的中点,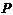 是
是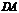 的中点,∴
的中点,∴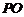 是△
是△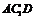 的中位线,知
的中位线,知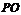 ∥
∥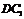 .
.
 而
而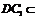 平面
平面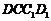 ,故
,故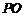 ∥平面
∥平面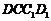 ;……(6分)
;……(6分)
(Ⅱ)由正方体的性质知:平面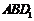 ⊥平面
⊥平面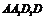 ,交
,交
线为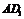 ,作
,作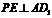 于
于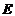 ,于是
,于是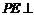 平面
平面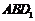 .连结
.连结
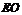 ,则
,则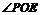 是
是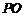 与平面
与平面 所成的角.设正方体棱
所成的角.设正方体棱
长为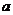 ,在
,在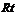 △
△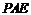 中,
中,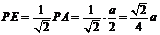 ,
,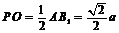 ,
,
∴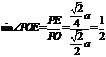 ,即
,即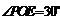 .故
.故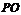 与平面
与平面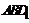 所成角的大小为
所成角的大小为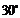 .…(12分)
.…(12分)
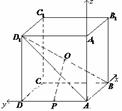 方法二:设正方体棱长为
方法二:设正方体棱长为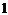 ,如图所示建立空间直角坐标系
,如图所示建立空间直角坐标系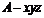 .由正方体的性质
.由正方体的性质
知: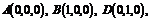
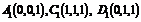 ,
,
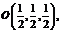
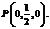 …………(2分)
…………(2分)
(Ⅰ)∵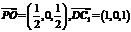 ,而
,而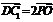 ,∴
,∴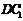 ∥
∥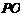
而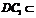 平面
平面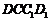 ,
,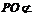 平面
平面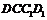 ,故
,故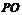 ∥平面
∥平面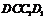 ;…(6分)
;…(6分)
(Ⅱ)∵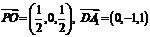 ,
,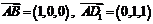 ,∴
,∴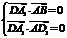 ,
,
∴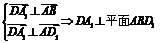 ,∴
,∴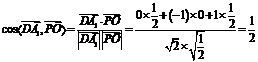 ,
,
∴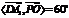 ,于是
,于是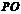 与平面
与平面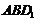 所成角的大小为
所成角的大小为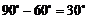 (12分)
(12分)
18.[解析](1)依题意得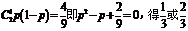 .又
.又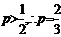 …(6分)
…(6分)
(2)记“该考生恰好参考5次后就中止参考”为事件C,由于该考生恰好参考5次后就中止参考,所以必然是最后两次测试均未通过,第三次测试通过,第一次、第二次中至少有一次通过,则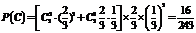 ,即该考生恰好参考5次后就中止考试的概率是
,即该考生恰好参考5次后就中止考试的概率是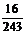 . ………………(12分)
. ………………(12分)
17.[解析](Ⅰ)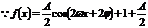 ,依题意
,依题意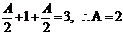 ,又
,又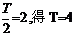
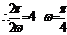 (3分),
(3分),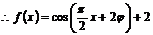 ,
,
令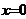 ,得
,得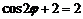
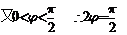
所以,函数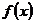 的解析式为
的解析式为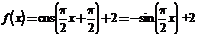 ……………(5分)
……………(5分)
(Ⅱ)由(Ⅰ)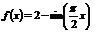 ,当
,当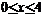 时,列表如下:
时,列表如下:
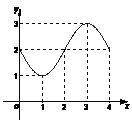

五个点为:(0,2),(1,1),(2,2),(3,3),(4,2).描点连线,
简图如右:(8分)由右图知,函数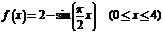 的
的
单调递减区间为:[0,1],[3,4];单调递增区间为:[1,3].…………(10分)
16. [答案]
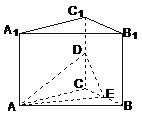
[答案]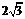 [解析]设正三棱柱
[解析]设正三棱柱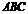 -
-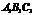 的侧棱长为
的侧棱长为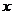 .取
.取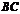 中点
中点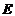 ,连结
,连结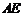 .∵
.∵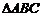 是正三角形,∴
是正三角形,∴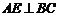 .又底面
.又底面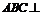 侧面
侧面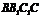 ,且两平面交线为
,且两平面交线为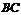 ,∴
,∴ 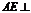 侧面
侧面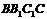 . 连结
. 连结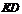 ,则
,则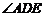 为直线
为直线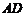 与侧面
与侧面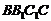 所成的角.∴
所成的角.∴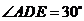 . 在
. 在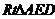 中,
中,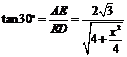 ,解得
,解得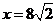 .∴此正三棱柱的侧棱长为
.∴此正三棱柱的侧棱长为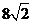 .
.
15.[答案]C[解析]法1: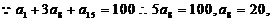
∴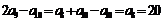 .故选C.
.故选C.
法2:由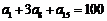 得
得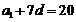 ,
,
∴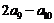 =
=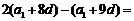
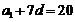 ,故选C.
,故选C.
14.[答案]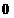 [解析]∵
[解析]∵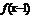 是定义在
是定义在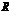 上的奇函数,∴
上的奇函数,∴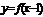 过
过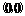 点,即
点,即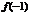
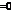 ,又
,又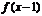 的周期为
的周期为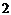 ,∴
,∴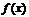 的周期也为
的周期也为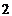 ,故
,故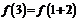
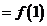
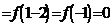 .
.
13.[答案]5[解析]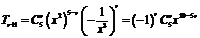 ,由
,由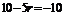 ,得
,得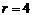 ,含有
,含有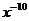 项为
项为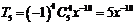 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com