2．(理科学生做)

袋子里有大小相同的3个红球和4个黑球，今从袋子里随机取球.

　　 (Ⅰ)若有放回地取3次，每次取1个球，求取出1个红球2个黑球的概率；

　　 (Ⅱ)若无放回地取3次，每次取1个球，

①求在前2次都取出红球的条件下，第3次取出黑球的概率；

②求取出的红球数的分布列和数学期望.

解：(Ⅰ)记“取出1个红球2个黑球”为事件A，根据题意有

；

答：取出1个红球2个黑球的概率是.　　　　　　　　　

(Ⅱ)①方法一：记“在前2次都取出红球”为事件B，“第3次取出黑球”为事件C，则，，所以.

方法二：.

答：在前2次都取出红球的条件下，第3次取出黑球的概率是.　

②随机变量的所有取值为.

，，

，.

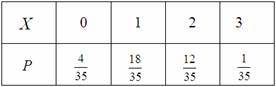
所以.　　　　　　

说明：首先让学生清楚有放回与无放回这两种模型的区别，应该清楚每种情况对应的基本事件空间是谁，同时要弄清楚序的问题，一个总的问题：分子和分母同时有序或无序.还要注意条件概率问题中的相关定义，谁是条件.

1．(理科学生做)

某班级举行一次知识竞赛活动，活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数，满分为100分)进行统计，制成如下频率分布表．

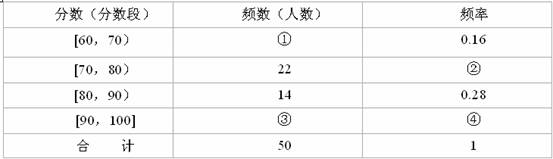
(Ⅰ)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案)；

(Ⅱ)决赛规则如下：参加决赛的每位同学依次口答4道小题，答对2道题就终止答题，并获得一等奖.如果前三道题都答错，就不再答第四题.某同学进入决赛，每道题答对的概率的值恰好与频率分布表中不少于80分的频率的值相同．

①求该同学恰好答满4道题而获得一等奖的概率；

②记该同学决赛中答题个数为，求的分布列及数学期望．

解：(Ⅰ) ① 　8 　　　② 0.44 　　　③ 6　 　　④ 　0.12

(Ⅱ)由(Ⅰ)得，P = 0.4

①该同学恰好答对4道题而获得一等奖，即前3道题中刚好答对1道题.第4道也能够答对才获得一等奖，则有

②答对2道题就终止答题，并获得一等奖，所以该同学答题个数为2、3、4.

即X= 2、3、4

分布列为：

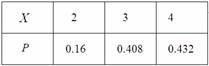
说明：本题考查统计问题：用样本估计总体，考查概率问题：满足特殊条件的概率的事件如何求其概率，要求同学 把条件真正弄清楚之后，再动手进行计算.同时还要求同学们分清一些典型的分布问题.

2. 数列满足，()

(Ⅰ) 当时，求及；

(Ⅱ)是否存在实数，使得数列为等差数列或等比数列？若存在，求出其通项公式，若不存在，说明理由；

解：(Ⅰ)

，故，所以.

(Ⅱ) ，

　，

　，

若数列为等差数列，则

方程没有实根，故不存在，使得数列为等差数列.

若数列为等比数列，则，即

解得：.

　 将个式子相加，，

又符合条件，　

，故数列为等比数列. 通项公式为

说明： 本题给出的是数列与两项之间的递推形式.在第二问中，通过特殊方法，得到的值，要注意引导学生理解结果并非充要条件，而是必要不充分条件，所以需要进一步的验证，而且在验证过程中，使用了叠加法，可以为学生说明其结构形式和解题策略要让学生掌握归纳的思想，学会从特殊到一般的思考数学问题的思维过程.

1. 设数列的前项和．

(Ⅰ)证明数列是等比数列；

(Ⅱ)若，且，求数列的前项和．

(Ⅰ)证：因为　　　　　　 ，

　　 ，

所以当时，，整理得.

由，令，得，解得.

所以是首项为，公比是的等比数列.

(Ⅱ)解：由，得

.

所以

从而 .

　　　 .

　　 说明：数列的与问题是数列的基本问题，通过两者之间的转化达到解决问题的目的是学生应该落实的.本题的第一问也可以改为“求数列的通项”或“求数列的前n项和”，提高思维的强度.

3. 如图，矩形ABCD内接于由函数图象围成的封闭图形，其中顶点C，D在上，求矩形ABCD面积的最大值.

解：由图，设A点坐标为,,则，由图可得，记矩形ABCD的面积为S，易得

令，得

所以，令，得，

因为，所以.

随t的变化情况如下表：

t
	+	0	-
		极大值

　　 由上表可知，当，即时， S取得最大值为，所以矩形ABCD面积的最大值为.

说明：本题主要是帮助学生经历根据问题的条件和要求建立函数的解析式及确定定义域再研究函数的变化状态的思维过程.

2. 设.

(I)求的单调区间与极值；

(II)求方程的实数解的个数.

解：(I)，由 得 或.

			--
	单增	极大值	单减	极小值	单增

所以，的单调递增区间为和，单调递减区间为；

极大值为，极小值为．

(II)由于，所以，.　

①　　 当时，，即是方程的一个解.

又因为，

所以,方程在内至少有一个解.根据函数单调性可知，方程有两个不同的解.

　　　 ②当时，，即是方程的一个解.

又因为，

所以方程在内至少有一个解.根据函数单调性可知，方程有两个不同的解.

③当时，，，所以方程在内至少有一个解. 又由，知方程在内至少有一个解；由，知方程在内至少有一个解.根据函数单调性可知，方程有三个不同的解.

　　 说明：通过本题考查学生几个方面的能力：

(1)能否将“求方程的实数解的个数”问题转化为函数的零点问题；

(2)对于函数问题，是否能够主动运用导数这一工具来研究函数整体的状态、性质.

1.已知函数

　 (Ⅰ)求的极值；

　 (Ⅱ)若函数的图象与函数的图象在区间上有公共点，求实数a的取值范围.

解：(Ⅰ)

令

当是增函数

当是减函数

∴

(Ⅱ)(i)当时，，由(Ⅰ)知上是增函数，在上是减函数.

又当时，

所以，的图象在上有公共点，等价于

解得_.

(ii)当时，上是增函数，

∴_,

所以原问题等价于

又∴无解

说明：此题主要考查学生研究函数方法的运用：给函数解析式之后，能否通过研究函数的工具导数研究函数的变化趋势，通过研究函数在区间的端点处的函数值或符号进一步了解函数的准确的变化状态.此题也可以做如下引申：“若函数的图象与函数的图象在区间上有两个公共点，求实数a的取值范围.”