22．解：(1)设点M的坐标为，相应的点P的坐标为，则，

直线PQ的方程为：，所以点Q的坐标为，

直线OP的方程为：，

所以点N的坐标为，

因此：，即：，………………………………………………4分

所以曲线C的方程为：，

即；…………………6分

　 (2)设存在定点使得，

设直线的方程为：，点

由得到，即，

　，

得到：，

即：，

即(1)………10分

由方程组：得到：，

即，

所以：且，代入(1)式得到：

，

要对满足且的实数恒成立，

只需要，即，

所以存在定点使得。……………………………12分

21．解：(1)，由条件得到：

，得到：……………………………………………6分

(2)依题意恒成立，令，则，所以，………………………………………………8分

因此：恒成立，即恒成立，

由得到：，………………………………………………………………10分

又因为：，所以恒成立，

所以：函数与函数的分界线方程是

。…………12分

20．解：⑴时，　　 两式相减得　

　　　 …………………4分

当时，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

则，数列的通项公式为　　　 ………………………………6分

⑵把数列的通项公式代入数列的通项公式，可得

=

　 =

……………………………10分

　 …………………………………………………………12分

19．解：(1)这4位员工中恰好有2位员工参观世博会的概率是：

；…………………6分

　 (2)消费金额恰好为11000元的概率是：

，

消费金额恰好为14000元的概率是：

。……10分

所以：这4位员工因参观世博会消费总金额不超过10000元的概率是：

……………12分

18．解法一：(1)设的中点为，

，，…………………2分

又是正三角形，，

平面，，……………5分

又，；……………………6分

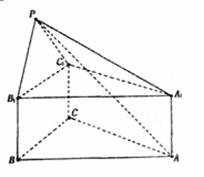
(2)平面平面，

平面，

又平面，四点共面，

过点作，垂足为点，则，

即为所求二面角的平面角，……………8分

由得到，

由得到，

又平面，，

，

，

所以所求二面角的大小是。……12分

解法二：(1)设的中点为，

，，…………………………………………………2分

又是正三角形，，

平面，，……………………………………5分

又，

；……………………………………6分

(2)平面平面，

平面，

又平面，四点共面，

如图，以点为坐标原点，所在直

线分别为轴，轴，轴，建立空间坐标系，

平面所在平面为坐标平面，取平面的

一个法向量…………………8分

由得到，

由得到，

点P的坐标为，点的坐标为，点的坐标为，

设平面的法向量为，

则，所以

　，所以，

令，则，…………………………………………10分

，

即所求二面角是。………………………………………………12分

17．解：(1)

所以当时，取最大值3，

此时，；…………………………………………………………5分

　 (2)由是的最大值及得到，，…… 7分

由余弦定理，

所以：，

所以，面积。……………………………10分

13．6；　　　 14．－3；　　 15．4；　　 16．(1)(4)

22．(本小题满分14分)

　　　 已知点P是圆上动点，以点P为切点的切线与轴相交于点Q，直线OP与直线相交于点N，若动点M满足：，记动点M的轨迹为曲线C。

　 (1)求曲线C的方程；

　 (2)若过点F(2，0)的动直线与曲线C相交于不在坐标轴上的两点A，B，设，问在轴上是否存在定点E，使得？若存在，求出点E的坐标，若不存在，说明理由。

楠杆高中2010年三轮复习模拟试题三

21．(本小题满分12分)

　　　 已知函数，在处取得极值，在处的切线与直线垂直。

　 (1)求常数的值；

　 (2)对于函数，若存在常数，对于任意，不等式都成立，则称直线是函数的分界线，求函数与函数的“分界线”方程。

20．(本小题满分12分)

　　　 已知有穷数列只有项(整数)，首项设该数列的前项和为，且，其中常数

　 (1)求的通项公式；

　 (2)若，数列满足，求证：