18、如图，正三棱柱 ABC-A₁B₁C₁中，AB=2, AA₁=1，

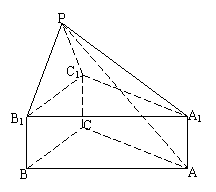点P在平面BCC₁B₁内，PB₁=PC₁=。

(1)求证：PA₁⊥BC; (2)求二面角C₁-PA₁-A。

17、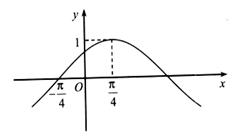已知函数，(其中)，其部分图像如图所示。

(1)求的解析式；

(2)求函数在

区间上的最大值及相应的值。

16、设函数的定义域为D，若存在非零数使得对于任意，有且，则称为M上的高调函数。现给出下列命题：①函数为R上的1高调函数；②函数为R上的高调函数；③如果定义域为的函数为上高调函数，那么实数的取值范围是。其中正确的命题是　　 。(写出所有正确命题的序号)

15、已知函数是奇函数且是上的增函数，若，满足不等式，则的最大值是　　　　

14、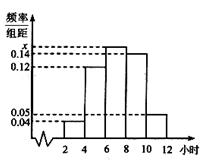某校为了解高三同学寒假期间学习情况，抽查了100名学生，统计他们每天平均学习时间，绘成频率分布直方图(如图)。则这100名同学中学习时间6~8小时的人数为　　　　　 。

13、已知向量=　　　　

12、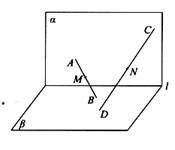如图，平面平面，=直线，A，C是内不同的两点，是内不同的两点，且A，B，C，D直线，M，N分别是线段AB，CD的中点。　　　 下列判断正确的是

A．当时，M，N两点不可能重合

B．当时，线段AB，CD在平面上正投影的长度不可能相等

C．M，N两点可能重合，但此时直线AC与不可能相交

D．当AB与CD相交，直线AC平行于时，直线BD可以与相交

11、

10、设表示，两者中的较小者，若函数，则满足的的集合为　

A． B．　 C． D．

9、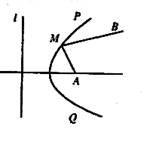如图，l表示南北方向的公路，A地在公路的正东2km处，B地在A地北偏东60°方向km处，河流沿岸PQ(曲线)上任一点到公路l和到A地距离相等，现要在河岸PQ上选一处M建一座码头，向A、B两地转运货物，经测算从M到A、B修建公路的费用均为a万元/km，那么修建这两条公路的总费用最低是

　 A．　 　B．5a　　 C．　 D．6a