5. 规律标志法

有些句子本身具有一定的标志，其语病往往就出现在那些有标志的部位，例如，有多个否定词的句子，往往出现否定不当的错误；有“能否”、“是否”等词语的句子，往往出现一面与两面不对应的错误；介词结构在句首的句子，往往出现介词结构掩盖主语的错误，等等。做题时，可根据这类句子的特点，顺藤摸瓜，准确地找到病症所在，从而做出准确的答案。

4. 逻辑分析法

有的语病不好从语法上查找，这时要从事理上对其进行分析，看其是否违反事理。进行逻辑分析，要注意从概念、判断和推理等多个侧面对句子进行分析，不可一叶障目。

3. 造句类比法

有的句子是否有语病，一时拿不定主意，这时仿照原句的结构另造一个常用的句子，经过分析比较，从而确定该句是否有语病。

2. 筋脉梳理法

纵观全局，运用语法手段，先理出句子的主干(主语、谓语、宾语)，审查句子的主干是否有搭配不当、成分残缺或赘余等错误；再清理句子的枝叶(补语、定语、状语)，仔细审查修饰成分内部是否有毛病，与中心语的搭配是否有毛病。

做辨析和修改病句题应注意并使用下列方法：

1. 语感审读法

在审读过程中，从对语言的感性认识上察觉语句有无毛病，如果觉得句子别扭，就再作分析比较，从而找到语病之所在。用这种办法做题，要做到胆大心细。胆大就是要相信自己的第一印象，心细就是要有仔细分析和查找语病的耐心。

《考试说明》对本能力点的要求是：能够“辨析并修改病句”，“能力层级D”。关于“病句类型”，《考试说明》规定了六种，即“语序不当、搭配不当、成分残缺或赘余、结构混乱、表意不明、不合逻辑”。

21. 本题(1)、(2)、(3)三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分.作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。

(1)(本小题满分7分)选修4-2：矩阵与变换

已知向量=，变换T的矩阵为A=，平面上的点P(1，1)在变换T

作用下得到点P′(3，3)，求A⁴.

(2)(本小题满分7分)选修4-4：坐标系与参数方程

直线与圆(>0)相交于A、B两点，设

P(－1，0)，且|PA|:|PB|=1:2，求实数的值

(3)(本小题满分7分)选修4-5：不等式选讲

对于x∈R，不等式|x－1|+|x－2|≥²+²恒成立，试求2+的最大值。

2010年龙岩市高中毕业班第二次质量检查

20. (本小题满分14分)已知是函数的一个极值点。

(Ⅰ)求；

(Ⅱ)若直线与函数的图象有3个交点，求的取值范围；

(Ⅲ)设=()++(6-+2()，，若

=0有两个零点，且，试探究值的符号

19. (本小题满分13分)已知、，椭圆C的方程为，、分别为椭圆C的两个焦点，设为椭圆C上一点，存在以为圆心的与外切、与内切

(Ⅰ)求椭圆C的方程；

(Ⅱ)过点作斜率为的直线与椭圆C相交于A、B两点，与轴相交于点D，若

求的值；

(Ⅲ)已知真命题：“如果点T()在椭圆上，那么过点T

的椭圆的切线方程为=1.”利用上述结论，解答下面问题：

已知点Q是直线上的动点，过点Q作椭圆C的两条切线QM、QN，

M、N为切点，问直线MN是否过定点？若是，请求出定点坐标；若不是，请说明理由。

18. (本小题满分13分)如图，由不大于n(n∈)的正有理数排成的数表，质点按

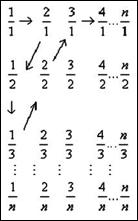
……顺序跳动，

所经过的有理数依次排列构成数列。

(Ⅰ)质点从出发，通过抛掷骰子来决定质点的跳动步数，

骰子的点数为奇数时，质点往前跳一步(从到达)；

骰子的点数为偶数时，质点往前跳二步(从到达).

①抛掷骰子二次，质点到达的有理数记为ξ，求Eξ；

②求质点恰好到达的概率。

(Ⅱ)试给出的值(不必写出求解过程)。