4．2009年“哥本哈根气候变化大会”全球瞩目，“低碳生活”将成为人类共同的选择。根据下图所示碳循环的部分过程进行的有关分析，正确的是

A. 参与②过程的生物包括生产者和分解者

B.　 ②增强后①随之增强，故不能通过增强②来减少大气中CO₂含量

C. 碳在生物群落与无机环境之间的循环主要是以含碳有机物的形式进行

D. 人类减少对化石燃料的依赖是当前缓解温室效应的重要措施

3. 下列关于基因的叙述，正确的是

A. 基因突变一定会改变生物的性状

B. 基因中碱基排列顺序改变一定会导致遗传信息改变

C. 基因控制生物的性状一定通过直接控制蛋白质的结构来实现

D. 基因频率改变一定会导致新物种产生

2. 某同学在上体育课进行剧烈运动时，需要通过一定机制来维持内环境的稳态。下列有关叙

述，不正确的是

A．维持体温的稳定是通过神经-体液调节

B. 大量流汗导致失水过多，通过抗利尿激素分泌减少进行调节

C. 葡萄糖消耗增多，血糖浓度降低，通过胰高血糖素分泌增加进行调节

D. 肌细胞无氧呼吸产生并释放到血液中的乳酸，由缓冲物质中和以维pH相对稳定

1. 下面以紫色洋葱鳞片叶表皮细胞为实验材料的有关叙述，正确的是

A. 表皮细胞较大易观察，可用于低温诱导染色体数目变化的实验

B. 表皮细胞含DNA和RNA，可用吡啰红使其DNA染成红色

C. 表皮细胞含有色素，可用于叶绿体色素的提取和分离实验

D. 表皮细胞具有大液泡，可用于观察植物细胞的吸水和失水实验

21. 本题(1)、(2)、(3)三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分.作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。

(1)(本小题满分7分)选修4-2：矩阵与变换

已知向量=，变换T的矩阵为A=，平面上的点P(1，1)在变换T

作用下得到点P′(3，3)，求A⁴.

(2)(本小题满分7分)选修4-4：坐标系与参数方程

直线与圆(>0)相交于A、B两点，设

P(－1，0)，且|PA|:|PB|=1:2，求实数的值

(3)(本小题满分7分)选修4-5：不等式选讲

对于x∈R，不等式|x－1|+|x－2|≥²+²恒成立，试求2+的最大值。

2010年龙岩市高中毕业班第二次质量检查

20. (本小题满分14分)已知是函数的一个极值点。

(Ⅰ)求；

(Ⅱ)若直线与函数的图象有3个交点，求的取值范围；

(Ⅲ)设=()++(6-+2()，，若

=0有两个零点，且，试探究值的符号

19. (本小题满分13分)已知、，椭圆C的方程为，、分别为椭圆C的两个焦点，设为椭圆C上一点，存在以为圆心的与外切、与内切

(Ⅰ)求椭圆C的方程；

(Ⅱ)过点作斜率为的直线与椭圆C相交于A、B两点，与轴相交于点D，若

求的值；

(Ⅲ)已知真命题：“如果点T()在椭圆上，那么过点T

的椭圆的切线方程为=1.”利用上述结论，解答下面问题：

已知点Q是直线上的动点，过点Q作椭圆C的两条切线QM、QN，

M、N为切点，问直线MN是否过定点？若是，请求出定点坐标；若不是，请说明理由。

18. (本小题满分13分)如图，由不大于n(n∈)的正有理数排成的数表，质点按

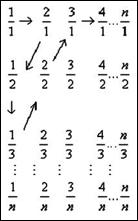
……顺序跳动，

所经过的有理数依次排列构成数列。

(Ⅰ)质点从出发，通过抛掷骰子来决定质点的跳动步数，

骰子的点数为奇数时，质点往前跳一步(从到达)；

骰子的点数为偶数时，质点往前跳二步(从到达).

①抛掷骰子二次，质点到达的有理数记为ξ，求Eξ；

②求质点恰好到达的概率。

(Ⅱ)试给出的值(不必写出求解过程)。

17. (本小题满分13分)如图，在正方体的上底面上叠放三棱柱

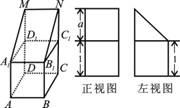
，该几何体的正视图与左视图如右图所示.

(Ⅰ)若，求实数的值；

(Ⅱ)在(I)的条件下：

① 证明平面；

②求直线与平面所成角的正弦值

16. (本小题满分13分)已知向量，，

定义函数=。

(Ⅰ)求的最小正周期；在所给的坐标系中作出函数，∈的图象

(不要求写出作图过程);

(Ⅱ)若=2，且14≤≤18，求的值