
1. 化简复数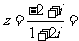
A.  B.
B. 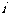 C.
C. 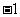 D.
D. 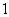
18.(I)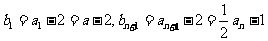 。……………………………………2分
。……………………………………2分
若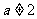 ,由
,由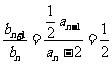 ,得数列
,得数列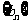 构成等比数列。…………………………… 3分
构成等比数列。…………………………… 3分
若a=2,b1=0,数列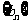 不构成等比数列。………………………………………………… 4分
不构成等比数列。………………………………………………… 4分
(II)由a1=1,得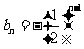 ………………………………………………………………5分
………………………………………………………………5分
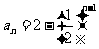 ……………………………………………………………………………… 6分
……………………………………………………………………………… 6分
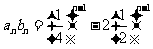 …………………………………………………………………… 7分
…………………………………………………………………… 7分

17.解(I)从这6名代表中随机选出2名,共有15种不同的选法,分别为(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)。…………………………………………………… 2分
其中代表A被选中的选法有(A,B),(A,C),(A,D),(A,E),(A,F)五种,…4分
则代表A被选中的概率为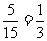 。………………………………………………………… 6分
。………………………………………………………… 6分
(II)解法一:随机选出的2名代表“恰有1名来自北美洲或2名都来自非洲”的结果
有9种,分别是(A,C),(A,D),(B,C),(B,D),(C,E),(C,F),(D,E),(D,F),(E,F)。………………………………………………………………………………… 9分
“怡有1名来自北美洲或2名都来自自非洲”,这一事件的概率为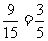 。………… 12分
。………… 12分
解法二:随机选出的2名代表“怡有1名来自北美洲”的结果有8种,概率为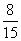 ;…8分
;…8分
随机选出的2名代表“都来自非洲”的结果有1种,概率为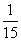 。…………………… 10分
。…………………… 10分
“恰有1名来自北美洲或都来自非洲”这一事件的概率为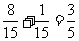 ……………… 12分
……………… 12分
13.8 14.-1 15.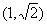 16.
16.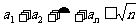
ABCBC BCDDA CA
22. (本小题满分14分)
已知函数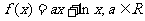 。
。
(I)求函数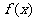 的极值;
的极值;
(II)对于曲线上的不同两点P1(x1,y1),P2(x2,y2),如果存在曲线上的点Q(x0,y0),且x1<x0<x2,使得曲线在点Q处的切线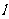 //P1P2的伴随切线。求证:曲线y=f(x)的任意一条弦均有伴随切线,并且伴随切线是唯一的。
//P1P2的伴随切线。求证:曲线y=f(x)的任意一条弦均有伴随切线,并且伴随切线是唯一的。
高三数学试题(文科·A)第4页(共 4页)
2010年高考训练
数学试题(文科·A)
21. (本小题满分12分)
已知焦点在x轴上,中心在坐标原点的椭圆C的离心率为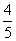 ,且过点
,且过点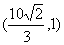 。
。
(I)求椭圆C的方程;
(II)直线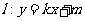 分别切椭圆C与圆
分别切椭圆C与圆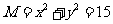 于A、B两点,求|AB|的值。
于A、B两点,求|AB|的值。
20. (本小题满分12分)
(本小题满分12分)
如图,等腰梯形ABEF中,AB//EF,AB=2,AD=AF=1
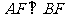 ,O为AB的中点,矩形ABCD所在的平面和平面ABEF互相垂直。
,O为AB的中点,矩形ABCD所在的平面和平面ABEF互相垂直。
(I)求证: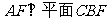 ;
;
(II)设FC的中点为M,求证:OM//平面DAF;
(III)求三凌锥C - BEF的体积。
19. (本小题满分12分)
已知函数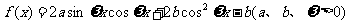 在
在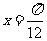 时取最大值2。
时取最大值2。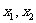 是集合
是集合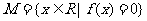 中的任意两个元素,|
中的任意两个元素,| |的最小值为
|的最小值为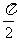 。
。
(I)求a、b的值;
(II)若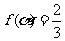 ,求
,求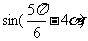 的值。
的值。
18. (本小题满分12分)
已知数列{an}的首项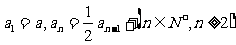 ,若
,若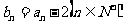
(I)问数列{bn}是否构成等比数列,并说明理由;
(II)若已知a1=1,设数列{an·bn}的前n项和为Sn,求Sn
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com