19.(本小题满分13分)

某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶，经过t小时与轮船相遇。

(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？

(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由。

18.(本小题满分13分)

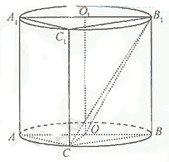
如图，圆柱OO₁内有一个三棱柱ABC-A₁B₁C₁，

三棱柱的底面为圆柱底面的内接三角形，且AB是圆O的直径。

(Ⅰ)证明：平面A₁ACC₁⊥平面B₁BCC₁；

(Ⅱ)设AB=AA₁。在圆柱OO₁内随机选取一点，记该点取自于

三棱柱ABC-A₁B₁C₁内的概率为P。

(i)　　　　　　　　　　 当点C在圆周上运动时，求P的最大值；

(ii)　　　　　 记平面A₁ACC₁与平面B₁OC所成的角为(0°< 　90°)。当P取最大值时，求cos的值。

17.(本小题满分13分)

已知中心在坐标原点O的椭圆C经过点A(2，3)，且点F(2.0)为其右焦点。

(Ⅰ)求椭圆C的方程；

(Ⅱ)是否存在平行于OA的直线L，使得直线L与椭圆C有公共点，且直线OA与L的距离等于4？若存在，求出直线L的方程；若不存在，说明理由。

16.(本小题满分13分)

设S是不等式x²-x-60的解集，整数m,nS。

(Ⅰ)记“使得m+n=0成立的有序数组(m,n)”为事件A，试列举A包含的基本事件；

(Ⅱ)设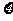=m²,求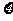的分布列及其数学期望E。

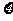15．已知定义域为(0，+)的函数f(x)满足：(1)对任意x(0, +),恒有f(2x)=2f(x)成立；(2)当x(1,2]时，f(x)=2-x。给出结论如下：

①对任意mZ,有f(2^m)=0；②函数f(x)的值域为[0，+ );③存在nZ,使得f(2ⁿ+1)=9;④“函数f(x)在区间(a,b)上单调递减”的充要条件是“存在kZ,使得(a,b) (2^k,2^k+1)”.

其中所有正确结论的序号是(　　 )。

14.已知函数f(x)=3sin(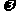x- 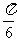)( 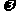>0)和g(x)=2cos(2x+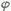)+1的图像的对称轴完全相同。若x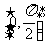,则f(x)的取值范围是(　　 )。

13.某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮。假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率等于(　　 )。

12.若一个底面是正三角形的三棱柱的正视图如图所示，则其表面积等于(　　 )。

11.在等比数列{a_n}中，若公比q=4，且前3项之和等于21，则该数列的通项公式a_n(　　 )

10.对于具有相同定义域D的函数f(x)和g(x)，若存在函数h(x)=kx+b(k,b为常数)，对任给的正数m，存在相应的x₀D，使得当xD且x>x₀时，总有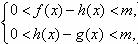则称直线l：y=kx+b为曲线y=f(x)与y=g(x)的“分渐近线”。给出定义域均为D=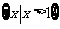的四组函数如下：

①f(x)=x²,g(x)= 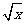;　　 ②f(x)=10^-x+2，g(x)= ;

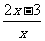③f(x)= 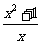,g(x)= 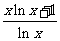;　　 ④f(x)= 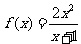，g(x)=2(x-1-e^-x).

其中，曲线y=f(x)与y=g(x)存在“分渐近线”的是

A．①④　　　　 B.②③　　　 C. ②④　　　 D. ③④

第Ⅱ卷 (非选择题 共100分)