
22.–Do you have to take _______ risk that you might lose all of your opportunity?
--Yes.Unless you put _________ end to the competition between us.
A.a; an B.the; an C.a; 不填 D.the ; 不填
第一节:单项选择 (共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21.–Andrew won’t like it , you know.
--_________________ ? I don’t care what Andrew thinks !
A.So what B.So where C.So why D.So how
22.(本小题满分12分)
已知抛物线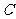 的顶点在原点
的顶点在原点 ,焦点与椭圆
,焦点与椭圆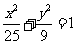 的右焦点重合.
的右焦点重合.
(Ⅰ)求抛物线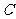 的方程;
的方程;
(Ⅱ)抛物线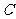 的轴上是否存在定点
的轴上是否存在定点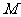 ,使过点
,使过点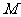 的动直线与抛物线
的动直线与抛物线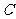 相交于
相交于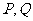 两点时,都有
两点时,都有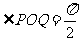 .若存在,求
.若存在,求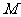 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
21.(本小题满分12分)
设函数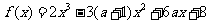 ,其中
,其中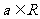 .
.
(Ⅰ)若 在
在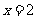 处的切线
处的切线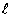 与直线
与直线 垂直,求切线
垂直,求切线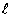 的方程;
的方程;
(Ⅱ)若 在
在 上不是单调函数,求
上不是单调函数,求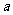 的取值范围.
的取值范围.
20.(本小题满分12分)
甲乙两队参加奥运知识竞赛,每队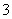 人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为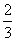 ,乙队中
,乙队中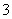 人答对的概率分别为
人答对的概率分别为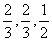 ,且各人正确与否相互之间没有影响.用
,且各人正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分.
(Ⅰ)求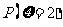 ;
;
(Ⅱ)用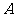 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于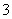 ”这一事件,用
”这一事件,用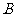 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求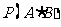 .
.
19.本小题满分12分)
设数列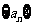 、
、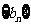 满足:
满足: 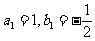 ,
, ,
,
(1)求数列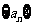 和
和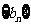 的通项公式;
的通项公式;
(2)若数列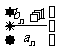 的前
的前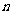 项和为
项和为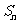 ,求
,求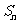 .
.
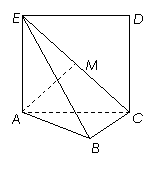
18.(本小题满分12分)
如图,正方形 所在的平面与平面
所在的平面与平面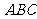 垂直,
垂直,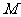 是
是 的中点,
的中点,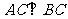 ,
,
且 .
.
(Ⅰ)求证: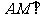 平面
平面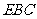 ;
;
(Ⅱ)求二面角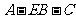 的大小.
的大小.

17.(本小题满分10分)
在△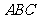 中,角
中,角 所对的边分别为
所对的边分别为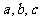 ,已知
,已知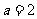 ,
, ,
,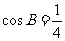 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求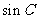 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com