
5、已知函数f(x)=log2(x2-ax-a)在区间(-∞,?1-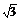 ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.
解:令g(x)=x2-ax-a,则g(x)=(x-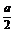 )2-a-
)2-a-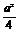 , 由以上知g(x)的图象关于直线x=
, 由以上知g(x)的图象关于直线x=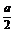 对称且此
对称且此
抛物线开口向上.因为函数f(x)=log2g(x)的底数2>1, 在区间(-∞,1-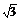 ]上是减函数,
]上是减函数,
所以g(x)=x2-ax-a在区间(-∞,1-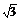 ]上也是单调减函数,且g(x)>0.
]上也是单调减函数,且g(x)>0.
∴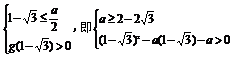
解得2-2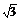 ≤a<2. 故a的取值范围是{a|2-2
≤a<2. 故a的取值范围是{a|2-2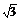 ≤a<2}.
≤a<2}.
4、设a>0,f(x)=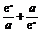 是R上的偶函数. (1)求a的值; (2)求证:f(x)在(0,+∞)上是增函数.
是R上的偶函数. (1)求a的值; (2)求证:f(x)在(0,+∞)上是增函数.
(1)解:
∵f(x)是R上的偶函数,∴f(-x)=f(x), ∴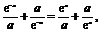
∴(a-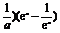 =0对一切x均成立, ∴a-
=0对一切x均成立, ∴a-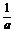 =0,而a>0,∴a=1.
=0,而a>0,∴a=1.
(2)证明 在(0,+∞)上任取x1、x2,且x1<x2,
则f(x1)-f(x2)=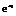 +
+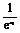 -
-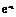 -
-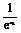 =
=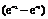 (
(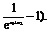
∵x1<x2,∴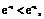 有
有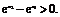 ∵x1>0,x2>0,∴x1+x2>0,∴
∵x1>0,x2>0,∴x1+x2>0,∴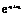 >1,
>1,
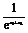 -1<0.∴f(x1)-f(x2)<0,即f(x1)<f(x2),故f(x)在(0,+∞)上是增函数.
-1<0.∴f(x1)-f(x2)<0,即f(x1)<f(x2),故f(x)在(0,+∞)上是增函数.
3、若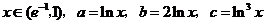 ,则( )
,则( )
A. <
<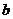 <
<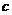 B.
B.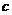 <
< <
<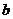 C.
C.
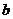 <
< <
<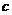 D.
D.
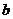 <
<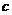 <
<
[解析]:由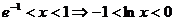 ,令
,令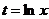 且取
且取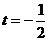 知
知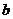 <
< <
<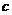
2、设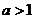 ,函数
,函数 在区间
在区间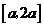 上的最大值与最小值之差为
上的最大值与最小值之差为 ,则
,则 ( )
( )
A.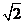 B.
B.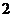 C.
C.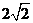 D.
D.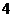
[解析]:设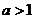 ,函数
,函数 在区间
在区间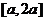 上的最大值与最小值分别为
上的最大值与最小值分别为
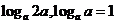 ,它们的差为
,它们的差为 , ∴
, ∴ 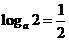 ,
, 4,选D。
4,选D。
[名师点睛]
指数函数,对数函数是两类重要的基本初等函数, 高考中既考查双基, 又考查对蕴含其中的函数思想、等价转化、分类讨论等思想方法的理解与运用. 因此应做到能熟练掌握它们的图象与性质并能进行一定的综合运用.
[试题演练]
1、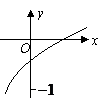 已知函数
已知函数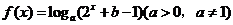 的图象如图所示,则
的图象如图所示,则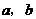 满足的关系是( )
满足的关系是( )
A.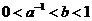 B.
B.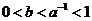
C.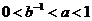 D.
D.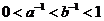
[解析]:由图易得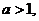
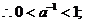 取特殊点
取特殊点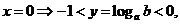
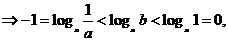
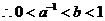 .选A.
.选A.
[点评]:本小题主要考查正确利用对数函数的图象来比较大小。
2、设二次函数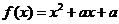 ,方程
,方程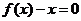 的两根
的两根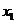 和
和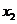 满足
满足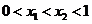 .(I)求实数
.(I)求实数 的取值范围;(II)试比较
的取值范围;(II)试比较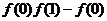 与
与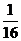 的大小.并说明理由.
的大小.并说明理由.
[解析]法1:(Ⅰ)令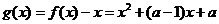 ,
,
则由题意可得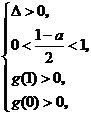
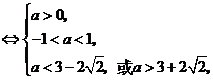
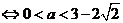 .
.
故所求实数 的取值范围是
的取值范围是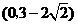 .
.
(II)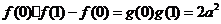 ,令
,令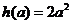 .
.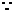 当
当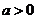 时,
时,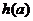 单调增加,
单调增加,
 当
当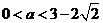 时,
时,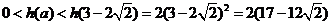
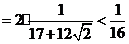 ,即
,即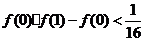 .
.
法2:(I)同解法1.
(II)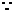
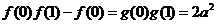 ,由(I)知
,由(I)知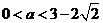 ,
,
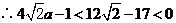 .又
.又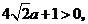 于是
于是
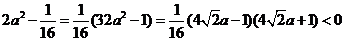 ,
,
即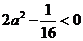 ,故
,故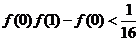 .
.
法3:(I)方程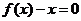
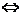
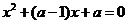 ,由韦达定理得
,由韦达定理得
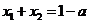 ,
,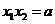 ,于是
,于是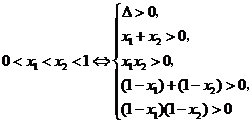
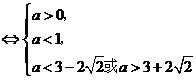
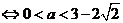 .故所求实数
.故所求实数 的取值范围是
的取值范围是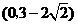 .
.
(II)依题意可设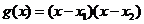 ,则由
,则由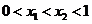 ,得
,得
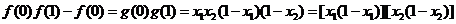
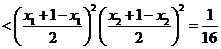 ,故
,故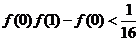 .
.
[点评]本小题主要考查二次函数、二次方程的基本性质及二次不等式的解法,考查推理和运算能力.
[名师点睛]
二次函数是中学代数的基本内容之一,它既简单又具有丰富的内涵和外延. 作为最基本的初等函数,可以以它为素材来研究函数的单调性、奇偶性、最值等性质,还可建立起函数、方程、不等式之间的有机联系;作为抛物线,可以联系其它平面曲线讨论相互之间关系. 这些纵横联系,使得围绕二次函数可以编制出层出不穷、灵活多变的数学问题. 同时,有关二次函数的内容又与近、现代数学发展紧密联系,是学生进入高校继续深造的重要知识基础. 因此,从这个意义上说,有关二次函数的问题在高考中频繁出现,也就不足为奇了.
学习二次函数,可以从两个方面入手:一是解析式,二是图像特征. 从解析式出发,可以进行纯粹的代数推理,这种代数推理、论证的能力反映出一个人的基本数学素养;从图像特征出发,可以实现数与形的自然结合,这正是中学数学中一种非常重要的思想方法.
[试题演练]
1、设二次函数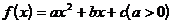 ,方程
,方程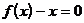 的两个根
的两个根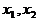 满足
满足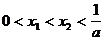 . 当
. 当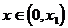 时,证明
时,证明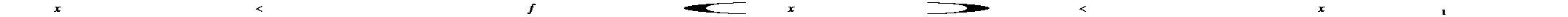 .
.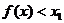
[解析]:在已知方程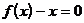 两根的情况下,根据函数与方程根的关系,可以写出函数
两根的情况下,根据函数与方程根的关系,可以写出函数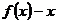 的表达式,从而得到函数
的表达式,从而得到函数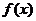 的表达式.
的表达式.
证明:由题意可知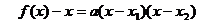 .
.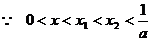 ,
,
∴ 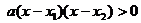 ,∴ 当
,∴ 当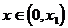 时,
时,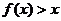 .
.
又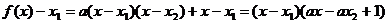 ,
,
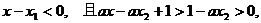 ∴
∴ 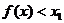 ,综上可知,所给问题获证.
,综上可知,所给问题获证.
[点评]:本题主要利用函数与方程根的关系,写出二次函数的零点式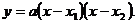 。
。
2.作出下列函数的图象. 
(1)y=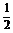 (lgx+|lgx|); (2)y=
(lgx+|lgx|); (2)y=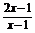 ; (3)y=
; (3)y=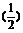 |x|.
|x|. 
解:(1)y=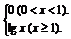

(2)由y=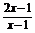 ,得y=
,得y=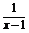 +2. 作出y=
+2. 作出y=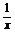 的图象,将y=
的图象,将y=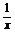 的图象向右平移一个单位,再向上平移2个单位得
y=
的图象向右平移一个单位,再向上平移2个单位得
y=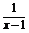 +2的图象.
+2的图象. 
(3)作出y=(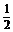 )x的图象,保留y=(
)x的图象,保留y=(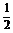 )x图象中x≥0的部分,加上y=(
)x图象中x≥0的部分,加上y=(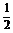 )x的图象中x>0的部分关于y轴的对称部分,即得y=(
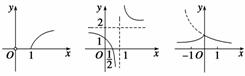
)x的图象中x>0的部分关于y轴的对称部分,即得y=(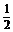 )|x|?的图象.其图象依次如下:
)|x|?的图象.其图象依次如下: 

[名师点睛]
图象变换:
①y = f(x)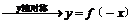 ②y =f(x)
②y =f(x)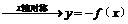

③y =f(x)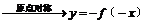 ④y=f(x)→y=f(|x|),把x轴上方的图象保留,x轴下方的图象关于x轴对称
④y=f(x)→y=f(|x|),把x轴上方的图象保留,x轴下方的图象关于x轴对称
⑤y=f(x)→y=|f(x)|把y轴右边的图象保留,然后将y轴右边部分关于y轴对称。(注意:它是一个偶函数)
⑥伸缩变换:y=f(x)→y=f(ωx), y=f(x)→y=Af(ωx+φ)具体参照三角函数的图象变换。
注:一个重要结论:若f(a-x)=f(a+x),则函数y=f(x)的图像关于直线x=a对称;
函数的图象是函数性质的直观载体,函数的性质可以通过函数的图像直观地表现出来。
因此,掌握函数的图像是学好函数性质的关键,这也正是“数形结合思想”的体现。复习函数图像要注意以下方面。1.掌握描绘函数图象的两种基本方法--描点法和图象变换法.2.会利用函数图象,进一步研究函数的性质,解决方程、不等式中的问题.3.用数形结合的思想、分类讨论的思想和转化变换的思想分析解决数学问题.4.掌握知识之间的联系,进一步培养观察、分析、归纳、概括和综合分析能力.
[试题演练]
1、“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则下图与故事情节相吻合的是
( )
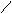

|


[解析]:选(B),在(B)中,乌龟到达终点时,兔子在同一时间的路程比乌龟短。
[点评]函数图象是近年高考的热点的试题,考查函数图象的实际应用,考查学生解决问题、分析问题的能力,在复习时应引起重视。
[名师点睛]
函数的性质是研究初等函数的基石,也是高考考查的重点内容.在复习中要肯于在对定义的深入理解上下功夫.复习函数的性质,可以从“数”和“形”两个方面,从理解函数的单调性和奇偶性的定义入手,在判断和证明函数的性质的问题中得以巩固,在求复合函数的单调区间、函数的最值及应用问题的过程中得以深化.具体要求是:1.正确理解函数单调性和奇偶性的定义,能准确判断函数的奇偶性,以及函数在某一区间的单调性,能熟练运用定义证明函数的单调性和奇偶性.2.从数形结合的角度认识函数的单调性和奇偶性,深化对函数性质几何特征的理解和运用,归纳总结求函数最大值和最小值的常用方法.3.培养学生用运动变化的观点分析问题,提高学生用换元、转化、数形结合等数学思想方法解决问题的能力.
[试题演练]
1设集合A={x|x<-1或x>1},B={x|log2x>0},则A∩B=( ) 
A.{x| x>1} B.{x|x>0} C.{x|x<-1}
D.{x|x<-1或x>1}
[解析]:由集合B得x>1 ,\ A∩B={x| x>1},故选(A)
。
[点评]本题主要考查对数函数图象的性质,是函数与集合结合的试题,难度不大,属基础题。
2设 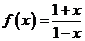 ,又记
,又记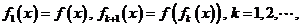 则
则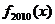 ()
()
A.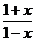 ;
B.
;
B.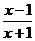 ;
C.
;
C.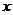 ;
D.
;
D.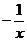 ;
;
[解析]:本题考查周期函数的运算。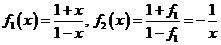 ,
,
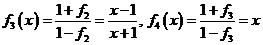 ,据此,
,据此,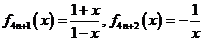 ,
,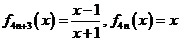 ,因2010为
,因2010为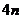 +2型,故选D.
+2型,故选D.
[点评]本题考查复合函数的求法,以及是函数周期性,考查学生观察问题的能力,通过观察,关于总结、归纳,要有从特殊到一般的思想。
3函数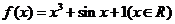 ,若
,若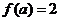 ,则
,则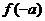 的值为( )
的值为( )
A.3
B.0
C.-1 D.-2
[解析]: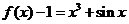 为奇函数,又
为奇函数,又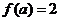

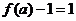 故
故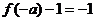 即
即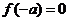 .
.
[点评]本题考查函数的奇偶性,考查学生观察问题的能力,通过观察能够发现如何通过变换式子与学过的知识相联系,使问题迎刃而解。
4设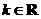 ,函数
,函数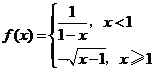 ,
,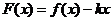 ,
,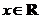 ,试讨论函数
,试讨论函数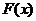 的单调性.
的单调性.
[解析]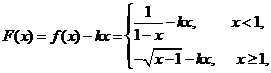
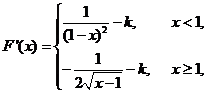

对于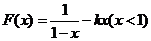 ,当
,当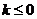 时,函数
时,函数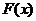 在
在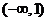 上是增函数;
上是增函数;
当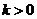 时,函数
时,函数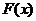 在
在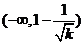 上是减函数,在
上是减函数,在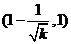 上是增函数;
上是增函数;
对于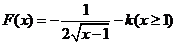 ,当
,当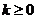 时,函数
时,函数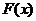 在
在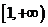 上是减函数;
上是减函数;
当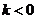 时,函数
时,函数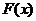 在
在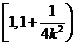 上是减函数,在
上是减函数,在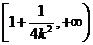 上是增函数。
上是增函数。
[点评]在处理函数单调性的证明时,可以充分利用基本函数的性质直接处理,但学习了导数后,函数的单调性就经常与函数的导数联系在一起,利用导数的性质来处理函数的单调进性,显得更加简单、方便。
5已知函数f(x)的定义域为R,且满足f(x+2)=-f(x)
(1)求证:f(x)是周期函数;(2)若f(x)为奇函数,
且当0≤x≤1时,f(x)=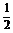 x,求使f(x)=-
x,求使f(x)=-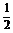 在[0,2010]上的所有x的个数.
在[0,2010]上的所有x的个数. 
(1)证明: ∵f(x+2)=-f(x), ∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),
∴f(x)是以4为周期的周期函数.
(2)解: 当0≤x≤1时,f(x)=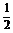 x, 设-1≤x≤0,则0≤-x≤1,∴f(-x)=
x, 设-1≤x≤0,则0≤-x≤1,∴f(-x)=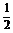 (-x)=-
(-x)=-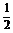 x.
x. 
∵f(x)是奇函数,∴f(-x)=-f(x), ∴-f(x)=-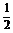 x,即f(x)=
x,即f(x)=
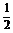 x.
x. 
故f(x)= 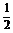 x(-1≤x≤1) 又设1<x<3,则-1<x-2<1, ∴f(x-2)=
x(-1≤x≤1) 又设1<x<3,则-1<x-2<1, ∴f(x-2)=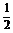 (x-2),
(x-2), 
又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x), 
∴-f(x)=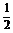 (x-2),
∴f(x)=-
(x-2),
∴f(x)=-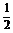 (x-2)(1<x<3). ∴f(x)=
(x-2)(1<x<3). ∴f(x)=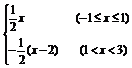

由f(x)=-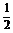 ,解得x=-1.
∵f(x)是以4为周期的周期函数. 故f(x)=-
,解得x=-1.
∵f(x)是以4为周期的周期函数. 故f(x)=-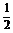 的所有x=4n-1
(n∈Z).
的所有x=4n-1
(n∈Z). 
令0≤4n-1≤2 009,则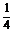 ≤n≤
≤n≤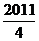 , 又∵n∈Z,∴1≤n≤502.75 (n∈Z),
, 又∵n∈Z,∴1≤n≤502.75 (n∈Z), 
∴在[0,2 010]上共有502个x使f(x)=-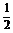 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com