
3、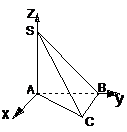 补充例题 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=
补充例题 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=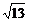 ,SB=
,SB=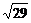

(1)求证:SC⊥BC;
(2)求SC与AB所成角的余弦值
解:如图,取A为原点,AB、AS分别为y、z轴建立空间直角坐标系,则有AC=2,BC=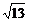 ,SB=
,SB=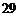 ,
,
得B(0,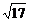 ,0)、S(0,0,2
,0)、S(0,0,2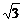 )、C(2
)、C(2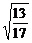 ,
, ,0),
,0),
∴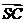 =(2
=(2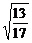 ,
, ,-2
,-2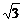 ),
), =(-2
=(-2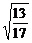 ,
,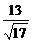 ,0)
,0)
(1)∵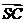 ·
· =0,∴SC⊥BC
=0,∴SC⊥BC
(2)设SC与AB所成的角为α,
∵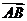 =(0,
=(0,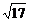 ,0),
,0),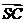 ·
·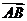 =4,|
=4,|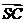 ||
||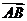 |=4
|=4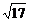 ,
,
∴cosα=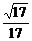 ,即为所求
,即为所求
练习:
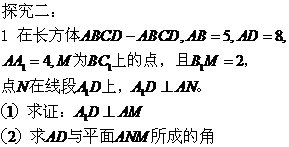

(答案见课件)

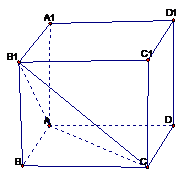
2、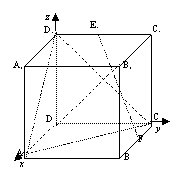 例2 在正方体
例2 在正方体 中, F分别是BC的中点,点E在D1C1上,且
中, F分别是BC的中点,点E在D1C1上,且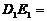
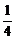 D1C1,试求直线E1F与平面D1AC所成角的大小
D1C1,试求直线E1F与平面D1AC所成角的大小
解:设正方体棱长为1,以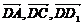 为单位正交基底,建立如图所示坐标系D-xyz
为单位正交基底,建立如图所示坐标系D-xyz
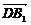 为D1AC平面的法向量,
为D1AC平面的法向量,
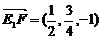
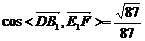
所以直线E1F与平面D1AC所成角的正弦值为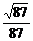
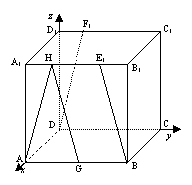
1、例1 在正方体 中,E1,F1分别在A1B1,,C1D1上,且E1B1=
中,E1,F1分别在A1B1,,C1D1上,且E1B1=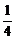 A1B1,D1F1=
A1B1,D1F1=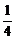 D1C1,求BE1与DF1所成的角的大小。
D1C1,求BE1与DF1所成的角的大小。
解1:(几何法)作平行线构造两条异面直线所成的角

解2:(向量法)设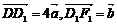 ,则
,则 且
且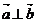
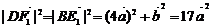
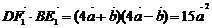
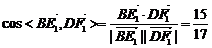
解3:(坐标法)设正方体棱长为4,以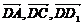 为正交基底,建立如图所示空间坐标系
为正交基底,建立如图所示空间坐标系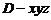
 ,
, ,
,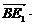
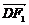 =15
=15
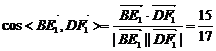
探究一:


(答案见课件)
2、数量积
(1)设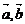 是空间两个非零向量,我们把数量
是空间两个非零向量,我们把数量 叫作向量
叫作向量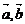 的数量积,记作
的数量积,记作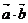 ,即
,即
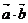 =
=
(2)向量的夹角:
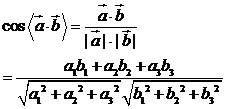
(2)若 ,
, ,则
,则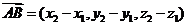 .
.
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。
2、法向量在求线面角中的应用:
原理:设平面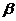 的斜线l与平面
的斜线l与平面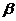 所的角为
所的角为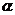 1,斜线l与平面
1,斜线l与平面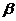 的法向量所成角
的法向量所成角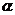 2,则
2,则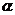 1与
1与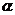 2互余或与
2互余或与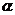 2的补角互余。
2的补角互余。
课前准备:
1、法向量在求面面角中的应用:
原理:一个二面角的平面角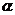 1与这个二面角的两个半平面的法向量所成的角
1与这个二面角的两个半平面的法向量所成的角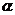 2相等或互补。
2相等或互补。
2、向量的夹角公式
1、异面直线所称的角、线面角的定义及求解方法
2、例5(2006年福建卷)如图,四面体ABCD中,O、E分别是BD、BC的中点,
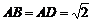
(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。

4、向量法在求点到平面的距离中
(1)设分别以平面外一点P与平面内一点M为起点和终点的向量为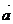 ,平面的法向量为
,平面的法向量为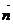 ,则P到平面的距离d等于
,则P到平面的距离d等于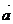 在
在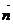 方向上正射影向量的模。
方向上正射影向量的模。
d=
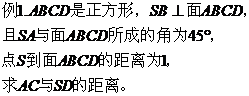

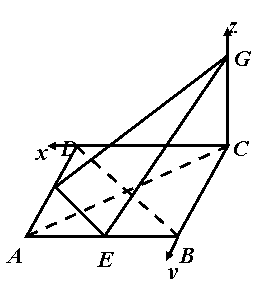
 例2、已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB、AD的中点,求点B到平面GEF的距离。
例2、已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB、AD的中点,求点B到平面GEF的距离。
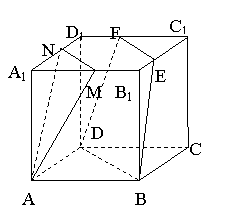
例3、在边长为1的正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点,求平面AMN与平面EFDB的距离。
例4 直三棱柱ABC-A1B1C1的侧棱AA1=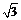 ,底面ΔABC中,∠C=90°,AC=BC=1,求点B1到平面A1BC的距离。
,底面ΔABC中,∠C=90°,AC=BC=1,求点B1到平面A1BC的距离。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com