2、向量法在求异面直线间的距离

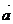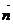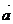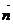设分别以这两异面直线上任意两点为起点和终点的向量为，与这两条异面直线都垂直的向量为，则两异面直线间的距离是在方向上的正射影向量的模。

d=　　　　　

1、两点间的距离公式

设空间两点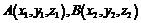，则

3、求空间中的距离有⑴直接法，即直接求出垂线段的长度；⑵转化法，转化为线面距或面面距，或转化为某三棱锥的高，由等积法或等面积法求解；⑶向量法求解。

2、距离的特征：⑴距离是指相应线段的长度；⑵此线段是所有相关线段中最短的；⑶除两点间的距离外，其余总与垂直相联系。

1、空间中的距离包括：两点间的距离，点到直线的距离，点到平面的距离，平行直线间的距离，异面直线直线间的距离，直线与平面的距离，两个平行平面间的距离。这些距离的定义各不相同，但都是转化为平面上两点间的距离来计算的。

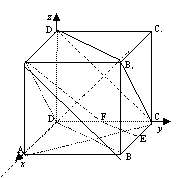
2、例4 　已知E,F分别是正方体的棱BC和CD的中点，求：(1)A₁D与EF所成角的大小；

(2)A₁F与平面B₁EB所成角的大小；

(3)二面角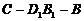的大小。

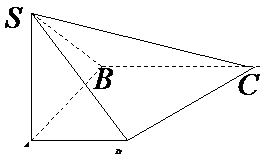
课　　 题：空间的距离

预习目标：

能用向量方法进行有关距离的计算

预习重、难点：向量方法求点到面的距离

预习过程

1、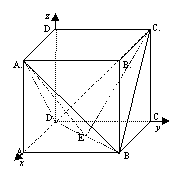例3 在正方体中,求二面角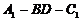的余弦值。

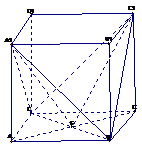
(法一)

(法二)

利用向量求二面角的大小。

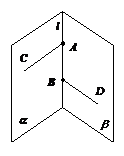方法一：转化为分别是在二面角的两个半平面内且与棱都垂直的两条直线上的两个向量的夹角(注意：要特别关注两个向量的方向)

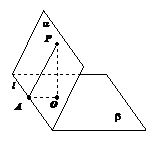
如图：二面角α-l-β的大小为θ，

A，B∈l，AC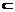α，BD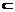β, AC⊥l，BD⊥l

则θ=<, >=<, >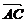　

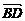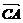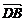方法二：先求出二面角一个面内一点到另一个面的距离及到棱的距离，然后通过解直角三角形求角。

图(1)　　　　　　　　 图(2)

如图(1)：已知二面角α-l-β，在α内取一点P，

过P作PO⊥β，及PA⊥l,连AO，

则AO⊥l成立，∠PAO就是二面角的平面角

用向量可求出|PA|及|PO|，然后解三角形PAO

求出∠PAO。

方法三：转化为求二面角的两个半平面的法向量夹角的补角。

如图(2)P为二面角α-l-β内一点，作PA⊥α，

PB⊥β，则∠APB与二面角的平面角互补。

2、平面的法向量的定义

1、二面角的定义及求解方法