
5.在等比数列{an}中,Sn表示前n项和,若a3=2S2+1,a4=2S3+1,则公比q=( )
A.3 B.-3 C.-1 D.1
4.数列{an}是公差不为零的等差数列,并且a5、a8、a13是等比数列{bn}的相邻三项,若b2=5,则bn=( )
A.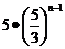 B.
B. C.
C.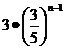 D.
D.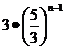
3.在正项等比数列{an}中,a1a2a3…a30=230,则a2a5a8…a29=( )
A.210 B.220 C.215 D.216
2.已知数列{an}是公比为q(q≠1)的等比数列,则数列:①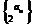 ②
②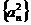 ③
③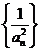 ④
④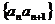 ⑤
⑤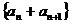 ,其中等比数列个数为( )
,其中等比数列个数为( )
A.2 B.3 C.4 D.5
1.等比数列{an}中,如果a6=6,a9=9,那么a3=( )
A.4 B.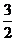 C.
C.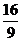 D.2
D.2
1、
起重机提起货物的时候,货物在钢绳拉力作用下上升一段距离,请同学们想:
a、钢绳对物体拉力的方向如何?物体的位移方向又如何?那么,钢绳的拉力对货物是否做了功?
b、但如果货物被拉到一定的高度后,起重机和货物共同沿水平方向前进了一段距离,则这段时间内钢绳对货物的拉力方向如何?货物的位移方向又如何?那么,这种情况钢绳的拉力对货物又是否做了功?
3、 理解正功、负功的概念
重点难点 功的概念(实际情况中如何理解力和力的方向上的位移)
学习过程 教材导读
2、明确功是标量,知道W=FLcosθ的适用范围,会用功的公式进行计算 
6.某工厂日生产某种产品最多不超过30件,且在生产过程中次品率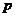 与日产量
与日产量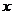 (
(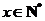 )
)
件间的关系为
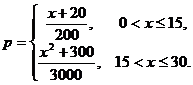
每生产一件正品盈利2900元,每出现一件次品亏损1100元.
(Ⅰ)将日利润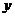 (元)表示为日产量
(元)表示为日产量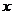 (件)的函数;
(件)的函数;
(Ⅱ)该厂的日产量为多少件时,日利润最大?
(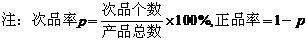 )
)
解:(Ⅰ)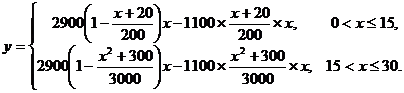
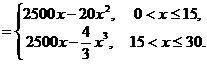 ……4分
……4分
(Ⅱ)当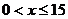 时,
时,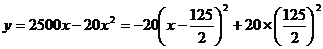 .
.
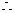 当
当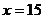 时,
时, 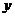 取得最大值33000(元).
……6分
取得最大值33000(元).
……6分
当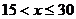 时,
时,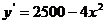 .
.
令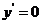 ,得
,得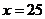 .
.
当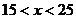 时,
时,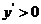 ;当
;当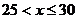 时,
时,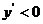 .
.
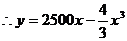 在区间
在区间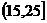 上单调递增,在区间
上单调递增,在区间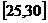 上单调递减. ……8分
上单调递减. ……8分
故当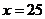 时,
时,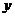 取得最大值是
取得最大值是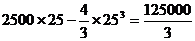 (元). ……10分
(元). ……10分
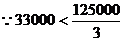 ,
,
 当
当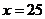 时,
时,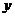 取得最大值
取得最大值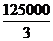 (元).
(元).
答: 该厂的日产量为25件时, 日利润最大.
考查意图:本小题主要考查函数和导数的应用,考查综合运用数学知识分析和解决实际问题能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com