2.行文凝练简约法

“废话多的地方，语言无力的地方，那么也就是思想腐朽的地方。”把这句话反过来理解并应用到议论文写作中，也就是说，要想在作品中表现出深邃的思想和独到的见解，就必须让语言精练有力。首先是不说废话。语言尽可能简洁，论题要明晰，论点要鲜明，不是为展示学问、卖弄见识。其次是尽可能使用整句。整句的优势在于概括力强。一组整句并列使用，其实际的语境意义要远远超过这些句子意义的简单相加。

2008年天津高考一考生在《人之常情》一文中写到：

①从古至今，情感与职责都是相辅相成的。两者间彼此融合，就可以达到无私、无畏、无悔、无怨的人生境界。想那苏武，在北国的彻骨寒风中坚守了十九载，吞毡饮雪而无怨无悔，不就是因为将个人情感与出使使命牢记心田，才坚忍执著、不屈不挠吗？一代名臣诸葛亮，“受任于败军之际，奉命于危难之间”，不也是既要报答刘备的知遇之恩，又要为天下苍生谋取利益吗？至于以直言敢谏而闻名天下的魏征，则更是凭借一颗赤诚之心，将个人情感与谏官职责发挥到了极致。情感与职责，在他们看来，似乎本为一体，无法分割。

②情感与职责相辅相成，最高境界便是无私、无畏、无悔、无怨。苏武牧羊，吞毡饮雪，因为爱国所以坚忍，因为履责所以不屈；诸葛亮临危受命，因为感恩所以无私，因为忧民所以无怨；魏征直言敢谏，因为忠君所以无悔，因为爱民所以无畏。情感与职责，在他们看来，似乎本为一体，无法分割。

这两段话，①段以散句为主，语言相对啰唆了点，也缺少了某种气势；而②段处理成整句后，不但语言精练，话语间蕴藏的气势也得到了加强。

1.正反对比法

是将两种性质截然相反或有差异的事物进行比较。在议论文写作时，运用对比式，就是把两种对立的事物或同一事物的互相矛盾的两个方面进行对照比较，肯定什么，否定什么，提倡什么，反对什么，就显得格外分明。具体地说，就是在论证过程中既要正面说理，又要反面阐述；在对比分析中，表明正确的观点。

例如2008年高考湖南模拟题作文中的两段文字：

希特勒、墨索里尼也许会有不少的崇拜者，但我相信他们所崇拜的只是这二位的政治才华和军事指挥能力，绝不会欣赏他们发动的战争给人类带来的伤害。希特勒、墨索里尼至多也就是以“有政治抱负的野心家”的身份载入史册，人们更多的是对他们鄙弃与否定。他们没有爱心，没有爱使他们的才能偏离了前进的轨道。他们的野心竟然用世界人民的鲜血来实现，他们的理想之路竟然用人肉之躯来铺砌。野蛮！残忍！

当肆虐的洪水无情地吞噬着大地，毁灭着生命。是那些被誉为“最可爱的人”的人民解放军战士怀着爱祖国、爱人民的心去征服那浩浩洪水。洪水终于收敛了它的任性，大自然在爱的感化下变得温柔了。没有这些可爱的人，我们能这样幸福地生活吗？他们可以躲回内陆，任那洪水翻腾，他们没有；他们可以不用拿自己的生命换取一位年过古稀的老农的生命，他们没有。这些，只因为他们有爱。

野蛮残忍的希特勒、墨索里尼，虽然具有相当的“政治才华和军事指挥能力”，但因为“他们发动的战争给人类带来的伤害”，所以得到的是人类对他们的“鄙弃与否定”。面对肆虐的洪水，人民子弟兵用爱心、用生命去征服洪水，于是，“洪水终于收敛了它的任性，大自然在爱的感化下变得温柔了”。两相对照，孰是孰非，何等鲜明！何等透辟！

22.已知双曲线的中心在原点，焦点F₁、F₂在坐标轴上，离心率为且过点(4，-)

(Ⅰ)求双曲线方程；

(Ⅱ)若点M(3,m)在双曲线上，求证：点M在以F₁F₂为直径的圆上；

(Ⅲ)求△F₁MF₂的面积.

21.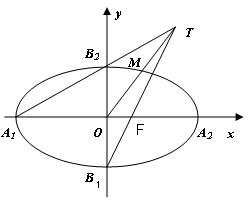如图，在平面直角坐标系中，为椭圆的四个顶点，为其右焦点，直线与直线相交于点T，线段与椭圆的交点恰为线段的中点，求该椭圆的离心率.

20.已知圆上的动点，点Q在NP上，点G在MP上，且满足.

　 (I)求点G的轨迹C的方程；

　 (II)点F(x,y)在轨迹C上，求2x²+y的最大值与最小值.

19．已知，椭圆C过点A，两个焦点为(－1，0)，(1，0)。

(Ⅰ) 求椭圆C的方程；　　　

(Ⅱ) E, F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。

18.已知点B(5,0)和点C(-5,0)，过点B的直线l与过点C的直线m相交于点A，设直线l的斜率为k₁，直线m的斜率为k_2:

(Ⅰ)如果k₁·k₂=,求点A的轨迹方程;

(Ⅱ)如果k₁·k₂=a,其中a≠0,求点A的轨迹方程,并根据a的取值讨论此轨迹是何种曲线.

17．已知p:2x²-9x+a<0,q:{x│x²-4x+3<0 且x²-6x+8<0},且┐p是┐q的充分条件，求实数a的取值范围。

16. 以知F是双曲线的左焦点，是双曲线右支上的动点，则的最小值为　　　　　　　　　　　　　　　　 .