例1　已知，则x的取值范围是_____．

　分析：利用指数函数的单调性求解，注意底数的取值范围．

　解：∵，

　∴函数在上是增函数．

　∴由，解得　．

　故 x的取值范围是．

　点评：利用指数函数的单调性解不等式，需将不等式两边都变成底数相同的指数式，并判断底数与1的大小，对于含有参数的要注意对参数进行讨论．

　例3　若关于x的不等式，则x的取值范围是_______.

　错解：如图3(1)，在同一坐标系内，分别作半椭圆，即和直线.

　由，得.

　∴原不等式的解集为.

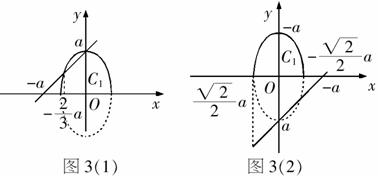　 　分析：错解在作图时，受椭圆中长半轴长a的影响，默认a>0，遗漏了a<0的情形.当a<0时，如图3(2)，x的取值范围是.综上可知，a＞0时，x的取值范围是；时，x的取值范围是

　评注：利用数形结合解题，有些情况下，符合题意的图形不止一个，作图过程中，极易只画出自己最习惯最熟悉的图形，从而导致作图不完备，考虑问题不周，以致求解出错.

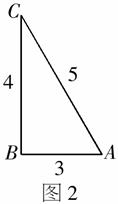　 　例2　已知平面上三点A、B、C满足，则的值等于______.

　错解：如图2，由条件知△ABC中，.

　∴

.

　分析：虽然这是一道基础题，但出错率相当高.究其原因是误以为与与的夹角就是三角形的内角C、A. 事实上，由向量夹角的定义应有

.

　评注：在转换过程中，倘若对一些基本概念理解不够深刻，就难免出错.

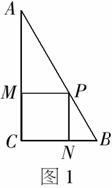　 　例1　(2005高考全国卷Ⅲ)已知在△ABC中，∠ACB=90°，BC=3，AC=4，P是AB上的点，则点P到AC、BC的距离乘积的最大值是______.

　错解：如图1，过P作PM⊥AC，PN⊥BC，则当四

边形PMCN为正方形时，点P到AC、BC的距离乘积取最

大值，此时可设PM=PN=x.

　由PM∥BC，得　，

　解得　.

　故所求最大值为.

　分析：默认四边形PMCN为正方形时得出本题的结论，只是从“形”的角度的猜想，并没有足够的理论依据.事实上，设P到AC、BC的距离分别为x(x≥0)和y(y≥0)，则，即.

　当时，xy取得最大值3.

　评注：在利用图形的直观性的同时，不能忽视必要的逻辑分析，必须有足够的理论依据才能确保结论的可靠性.

5.已知点在第一象限，则在内的取值范围是(　).

　(A)　　　　 　(B)

　(C)　　　 　(D)

4.函数的图象与直线及x轴所围成图形的面积称为函数在上的面积.已知函数在，上的面积为，则：

　(1)函数在上的面积为______；

　(2)函数在上的面积为_____.

3.已知，存在实数t，使得当时，恒成立，则m的最大值为(　).

　(A)3　(B)4　(C)5　(D)6

2.设函数，若，则的取值范围是(　)

　(A)　　　　　　　　 　　　　　　　　　 (B)

　(C)　　　　 　 (D)

　习题

1.设集合，集合，集合M∩N＝(　)

　(A)　　　　　 　(B)

　(C)　　　　　 　(D)

例3　 命题：若，则是的充分不必要条件．命题：函数的定义域是，则(　　 )

A．“或”为假　　　　　 B．“且”为真

C．真假　　　　　　　　　　　　　　 D．假真

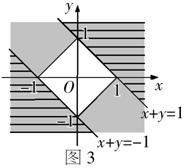　 解析：如图3，分别在同一直角坐标系中画出和所表示区域，前者是图3中正方形外的部分，而后者是直线的右上方与

的左下方的部分，由图可知，能推出

，而不能推出，故

是的必要不充分条件，命题是假命题．

不难求求得也为假命题，故选(A)．

评注：若所求问题中的等式或代数式的结构含有明显的几何意义，如时是个封闭的几何图形)等等，往往利用它们的图象解决更加简便．