
2. 关于叶肉细胞在光照条件下产生ATP的描述,正确的是
A.无氧条件下,光合作用是细胞ATP的唯一来源
B.无氧条件下,线粒体、叶绿体和细胞质基质都能产生ATP
C.线粒体和叶绿体合成ATP都依赖氧
D.细胞质中消耗的ATP均来源于线粒体和叶绿体
1. 右图表示酶活性与温度的关系。下列叙述正确的是
A.当反应温度由t2调到最适温度时,酶活性下降
B.当反应温度由t1凋到最适温度时,酶活性上升
C.酶活性在t2时比t1高,故t1时更适合酶的保存
D.酶活性在t1时比t2低,表明t1时酶的空间结构破坏更严重
例3 实数 满足
满足 ,则使
,则使 恒成立的
恒成立的 的取值范围为___ __.
的取值范围为___ __.
解析:此题主元是 ,参数是
,参数是 ,照惯例不等式变为:
,照惯例不等式变为: ,再设
,再设 ,
, ,构造直曲相关问题求参.此种方法解答起来比较麻烦.
,构造直曲相关问题求参.此种方法解答起来比较麻烦.
现在调整思维角度,视 为主元,则问题变为求
为主元,则问题变为求 的取值范围,使原不等式在
的取值范围,使原不等式在 上恒成立.这就非常简捷了,因为曲线已转化为直线.即由原不等式,得
上恒成立.这就非常简捷了,因为曲线已转化为直线.即由原不等式,得 ,图象为一条直线(图略),则欲使当
,图象为一条直线(图略),则欲使当 时
时 恒成立,只须
恒成立,只须 由此解得
由此解得 ,或
,或 ,此即所求范围.
,此即所求范围.
例2 当 时,关于
时,关于 的方程
的方程 根的个数为_____.
根的个数为_____.
解析:原方程为 ,即
,即 ,若直接构图,问题即为讨论直线
,若直接构图,问题即为讨论直线 与抛物线(弧)
与抛物线(弧) 的关系.因为直线是倾斜的,当其与抛物线相切时得用判别式求
的关系.因为直线是倾斜的,当其与抛物线相切时得用判别式求 的值.接下来还得按
的值.接下来还得按 分类,确定方程根的个数.
分类,确定方程根的个数.
这种数形结合方式的运算,主要是在求当直线与曲线相切时 的值,须化成一元二次方程,用判别式解决,不算太简捷.如若调整思维,联想到方程
的值,须化成一元二次方程,用判别式解决,不算太简捷.如若调整思维,联想到方程 等价于
等价于 ,于是有另一种构图方式.其简捷之处在于直线不是倾斜的而是平行于
,于是有另一种构图方式.其简捷之处在于直线不是倾斜的而是平行于 轴.
轴.
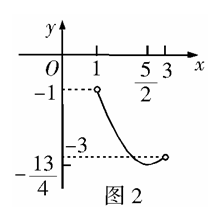 ∵
∵ ,如图2,借助图形可知,当
,如图2,借助图形可知,当 ,或
,或 时,方程只有一解;当
时,方程只有一解;当 时,方程有两解;当
时,方程有两解;当 或
或 时,方程无解.故应填1.
时,方程无解.故应填1.
例1 对任意角 ,
, 恒成立,则
恒成立,则 的取值范围是_____.
的取值范围是_____.
解析:对此题通常是变 为
为 ,整理成降幂排列式:
,整理成降幂排列式: ,于是一个二次不等式便显露出来了,便可建构曲线:令
,于是一个二次不等式便显露出来了,便可建构曲线:令 ,则
,则 ,这就需要分对称轴
,这就需要分对称轴 在区间
在区间 的左侧、内部、右侧三种情况构图求解.
的左侧、内部、右侧三种情况构图求解.
 因为需要讨论三种情况,显然较繁.现在我们做如下调控:既然问题是求
因为需要讨论三种情况,显然较繁.现在我们做如下调控:既然问题是求 的取值范围,使不等式
的取值范围,使不等式 在
在 上恒成立,于是可将不等式变为
上恒成立,于是可将不等式变为 ,这样可建构直曲相关的图形求解,比前一种方法简捷多了.
,这样可建构直曲相关的图形求解,比前一种方法简捷多了.
设 ,
, ,
, ,则后者为过定点
,则后者为过定点 的直线.如图1,欲使
的直线.如图1,欲使 在
在 上恒成立,只须
上恒成立,只须 ,即
,即 便可.
便可.
例8 已知a、b、c是某一直角三角形的三边的长,其中c为斜边,若点(m,n)在直线ax+by+2c=0上,则 的最小值等于_____.
的最小值等于_____.
解析:令 ,则d表示点(m,n)与坐标原点之间的距离.由于点(m,n)在直线ax+by+2c=0上,所以d的最小值就是坐标原点到直线ax+by+2c=0的距离
,则d表示点(m,n)与坐标原点之间的距离.由于点(m,n)在直线ax+by+2c=0上,所以d的最小值就是坐标原点到直线ax+by+2c=0的距离 ,即
,即 的最小值等于4.
的最小值等于4.
例9
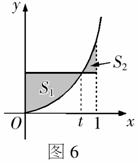 在区间
在区间 上给定曲线
上给定曲线 ,试在此区间内确定点t
,试在此区间内确定点t
的值,使图6中的阴影部分的面积 与
与 之和最小.
之和最小.
解: 面积等于边长为t与
面积等于边长为t与 的矩形的面积去掉曲线
的矩形的面积去掉曲线 与x轴、直线
与x轴、直线 围成的面积,即
围成的面积,即 的面积等于曲线
的面积等于曲线 与x轴、
与x轴、 围成的面积去掉矩形面积,矩形边长分别为
围成的面积去掉矩形面积,矩形边长分别为 ,即
,即 .
.
所以阴影部分面积S为:

由 ,得 t=0,或
,得 t=0,或 .
.
经验证知,当 时,
时, 最小.
最小.
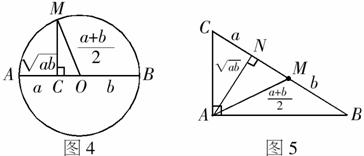 例7 如图4,请你观察图形以及图形中线段的位置关系及其数量关系,说明如何通过该图形来说明不等式
例7 如图4,请你观察图形以及图形中线段的位置关系及其数量关系,说明如何通过该图形来说明不等式 成立.你还能构造另外的图形来说明这个不等式成立吗?
成立.你还能构造另外的图形来说明这个不等式成立吗?
解析:在圆O中,AB是一条直径,M是圆上任意一点,过M点作MC⊥AB交AB于C,令CA=a,CB=b,则容易得到 ,由于在Rt△MCO中,MO是斜边,MC是直角边,所以有
,由于在Rt△MCO中,MO是斜边,MC是直角边,所以有 ;又当C点与O点重合时,有
;又当C点与O点重合时,有 ,故有
,故有 .由于问题的本质上是在Rt△AMB中处理问题,所以可构造类似的图形如图5所示(注:
.由于问题的本质上是在Rt△AMB中处理问题,所以可构造类似的图形如图5所示(注: .).
.).
评述:几何图形的直观解释和证明,真正体现了代数和几何的有机统一,可谓“无字的证明”.
由于数列的通项公式和前n项和公式都可以看成n的函数,因此,许多数列问题可以借助函数的图象解决.
例5 设 是公差为d的等差数列,
是公差为d的等差数列, 是前n项的和,且
是前n项的和,且 ,则下列结论错误的是( ).
,则下列结论错误的是( ).
(A) (B)
(B)
(C) (D)
(D) 和
和 均为
均为 的最大值
的最大值
解析:可以把等差数列的前n项和 看成是关于n的二次函数,结合图形可知,答案为(C).
看成是关于n的二次函数,结合图形可知,答案为(C).
例6 已知在等差数列 中,
中, ,前n项和为
,前n项和为 ,且
,且 .则当
.则当 取到最值时,n等于( )
取到最值时,n等于( )
 (A)6 (B)7 (C)12 (D)13
(A)6 (B)7 (C)12 (D)13
解析:由于 ,所以
,所以 ,而
,而
 ,所以数列的公差d<0,即数列是递减数列.
,所以数列的公差d<0,即数列是递减数列.
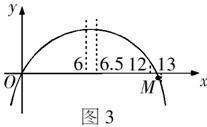
则 ,如图3,可以把
,如图3,可以把
看成关于n的二次函数,其图象是一条抛物线,经过原点,开口向下,又 ,所以若设抛物线和x正半轴的交点为
,所以若设抛物线和x正半轴的交点为 ,则12<m<13,于是抛物线的对称轴为
,则12<m<13,于是抛物线的对称轴为 ,因此当n=6时
,因此当n=6时 取到最大值,选(A).
取到最大值,选(A).
编者注:数列的有关问题用函数的观点来解决是一种较好的方法,但要注意,他们并非真正意义上的一次、二次函数!
我们学过的一些初等函数,如:正比例、反比例函数、一次函数、二次函数、指数函数、对数函数、三角函数等都蕴含着丰富的数形结合的思想,因此,在处理函数问题时,要充分联系函数图象.
例4 (2006年辽宁高考题)已知函数 ,则
,则 的值域是( ).
的值域是( ).
(A) (B)
(B) (C)
(C) (D)
(D)
解析: ,即等价于
,即等价于 ,因此在同一坐标系下分别画出函数
,因此在同一坐标系下分别画出函数 的图象,在两个图象的每两个交点之间取位于下方的图象,就是函数
的图象,在两个图象的每两个交点之间取位于下方的图象,就是函数 的图象,从而容易得到
的图象,从而容易得到 的值域是
的值域是 ,故答案为(C).
,故答案为(C).
在研究某些方程的根的个数问题、根的大小问题以及根的取值范围等问题时,都可以将方程进行恰当的变形,通过引进函数,转化为两个或几个函数图象之间的关系来解决.
例2 已知函数 ,若
,若 是方程
是方程 的两个根,则实数
的两个根,则实数 之间的大小关系是( ).
之间的大小关系是( ).
(A) (B)
(B)
(C) (D)
(D)
解析:若令 ,显然函数
,显然函数 的两个零点是a、b,函数
的两个零点是a、b,函数 的两个零点是
的两个零点是 ,而函数
,而函数 的图象是由函数
的图象是由函数 的图象沿y轴向上平移两个单位得到的,结合图象可知
的图象沿y轴向上平移两个单位得到的,结合图象可知 ,故应选(B).
,故应选(B).
例3 若方程 恰有4个不同的实数根,则实数m 的取值范围为_____.
恰有4个不同的实数根,则实数m 的取值范围为_____.
 解析:将方程化为
解析:将方程化为 ,构造函数
,构造函数
 ,则方程
,则方程
恰有4个不同的实数根,亦即两个函数 与
与 的图
的图
象恰好有4个不同的交点,如图2,易知当 4<m<0时
4<m<0时
方程有4个根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com