
处理集合与集合的关系,借助图形进行直观思考,不仅可以使各集合之间的相互关系直观明了,而且也便于将各元素的归属确定下来,使抽象的集合问题,形象直观的得解.
 例1 设
例1 设 ,则使
,则使 成立的实数m的取值范围是_____.
成立的实数m的取值范围是_____.
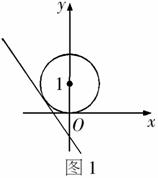
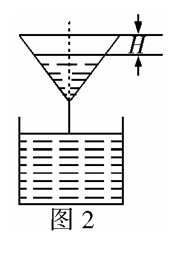
解析:由于集合A,B都是点的集合,故可结合图
形进行分析.集合A是圆 上的点的集合,
上的点的集合,
集合B是不等式 表示的平面区域内的点的
表示的平面区域内的点的
集合,要使 ,则应使圆被平面区域所包含(如图1),
,则应使圆被平面区域所包含(如图1),
知直线 应与圆相切或相离且在圆的下方,即
应与圆相切或相离且在圆的下方,即
 .当直线与圆相切时有
.当直线与圆相切时有 ,解得
,解得 ,故m的取值范围是
,故m的取值范围是 .
.
评述:如果所给集合是点的集合,那么在研究它们之间的关系时,可以借助数形结合思想,将问题转化为函数图象或曲线之间的关系求解.
例3 (2005年上海春招理16题)设定义域为R的函数 ,则关于x的方程
,则关于x的方程 有7个不同实数解的充要条件是( ).
有7个不同实数解的充要条件是( ).
 (A)b<0且c>0 (B)b>0且c<0
(A)b<0且c>0 (B)b>0且c<0
(C)b<0且c=0 (D)b≥0且c=0
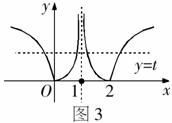
解析: 
其图象如图3所示, 的图象关于
的图象关于 对称,且
对称,且 .
.
若方程 ①有7个不同实数根,则方程
①有7个不同实数根,则方程 ②有两个不相等的实根,且一根为正,一根为0,否则,若方程②有两个相等的非负实根,则方程①至多有4个解,若方程②有两个不相等的正实根,则方程①有8个解.
②有两个不相等的实根,且一根为正,一根为0,否则,若方程②有两个相等的非负实根,则方程①至多有4个解,若方程②有两个不相等的正实根,则方程①有8个解.
因为 满足方程①,则
满足方程①,则 ,又
,又 也满足方程①,所以
也满足方程①,所以 .所以b<0,且c=0,故选(C).
.所以b<0,且c=0,故选(C).
点评:在中学阶段所涉及的函数:正、反比例函数,一次、二次函数,指数、对数函数等都要充分联系函数图象,借助图象的直观形象,达到求解的目的.
例4 设方程 的解为
的解为 ,方程
,方程 的解为
的解为 ,求
,求 .
.
分析:给出的 是不定的,所求得的
是不定的,所求得的 都不固定.但原方程可分别变形为
都不固定.但原方程可分别变形为 和
和 .因为
.因为 与
与 互为反函数,所以函数
互为反函数,所以函数 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,而
对称,而 可分别看作直线
可分别看作直线 与函数
与函数 的图象及函数
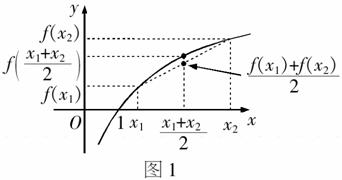
的图象及函数 的图象交点的横坐标.如图4,直线
的图象交点的横坐标.如图4,直线 与直线
与直线 互相垂直,点A与点B关于直线
互相垂直,点A与点B关于直线 对称,设点P为线段
对称,设点P为线段 的中点,且点
的中点,且点 为直线
为直线 与直线
与直线 的交点,则问题可转化为求点P的横坐标.
的交点,则问题可转化为求点P的横坐标.
 解:如图4,由
解:如图4,由 ,解得
,解得 则
则 .
.
评注:隐性条件的挖掘是解题的关键,要善于从条件的结构特征中寻找一些和函数图象关联的信息源,以便为解决问题作好形的铺垫.
例2 (2006年全国Ⅱ理科12题)函数 的最小值为( ).
的最小值为( ).
(A)190 (B)171 (C)90 (D)45
解析:绝对值往往是使试题增加难度的“添加剂”.如果试图进行分类讨论,几乎不可能完成,必须另寻妙法 的几何意义是什么?是数轴上的点
的几何意义是什么?是数轴上的点
 到点1的距离,那么
到点1的距离,那么 就是点x到点1与到点2的距离之和,如图2,当
就是点x到点1与到点2的距离之和,如图2,当 时,
时, 的最小值为1;又当x=2时,
的最小值为1;又当x=2时, 的最小值为2;…,依次类推,当x=10时,所求最小值为
的最小值为2;…,依次类推,当x=10时,所求最小值为 ,故选(C).
,故选(C).
求等差数列前9项的和当然是“小菜一碟”,而此时绝对值的几何意义则成了解题的关键,这个解题过程可用“一点突破,全线贯通”来形容!
例1 (2005年北京卷13题)对于函数 定义域中任意的
定义域中任意的 ,有如下结论:
,有如下结论:
① ;②
;② ;
;
③ ;④
;④ .
.
 当
当 时,上述结论中正确结论的序号是___.
时,上述结论中正确结论的序号是___.
解析:作出图象如图1,由图可知④不正确;而①显然不成立;②为运算律,成立;③表示 与
与 同号,由增函数的定义知:
同号,由增函数的定义知: 在其定义域上为增函数成立.所以答案为:②③.
在其定义域上为增函数成立.所以答案为:②③.
点评:本题综合考查函数的概念、图象及性质,选项③侧重考查单调性,选项④考查函数图象,若用代数方法研究,难度较大,通过图象的特征及其变化趋势则容易判断.
借助于函数的图象或方程的曲线,引入不等式(或方程)的图象,可以有效地审清题意,简化求解过程,并检验所得的结果.
在中学数学中,数形结合的思想体现的最充分的内容是解析几何.此外,函数与图象之间,复数与几何之间的相互转化也充分体现了数形结合的思想.
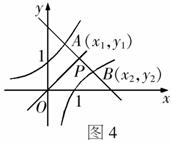
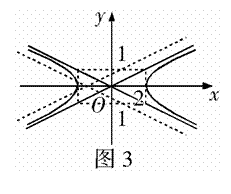 例4 已知直线
例4 已知直线 和双曲线
和双曲线 只有一个公共点,则k的不同取值有( ).
只有一个公共点,则k的不同取值有( ).
(A)1个 (B)2个 (C)3个 (D)4个
解析:如图3, 的图象是过定点
的图象是过定点 的直线系,双曲线的渐近线方程为
的直线系,双曲线的渐近线方程为 .
.
故过点 且和渐近线平行的直线与双曲线有且仅有一个公共点,此时
且和渐近线平行的直线与双曲线有且仅有一个公共点,此时 取两个不同的值.此外,过点
取两个不同的值.此外,过点 且和双曲线相切的直线与双曲线有且仅有一个公共点,此时
且和双曲线相切的直线与双曲线有且仅有一个公共点,此时 取两个不同的值,故正确答案为(D).
取两个不同的值,故正确答案为(D).
数形结合的核心是“数”与“形”的对应关系,熟知这些对应关系,沟通两者之间的联系,才能把握住每一个研究对象在数量关系上的性质与相应的图形的特征之间的联系,以求相辅相成,相互转化.
例3 如图2,液体从一圆锥形漏斗注入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟注完.已知圆柱中液面上升的速度是一个常量, 是圆锥形漏斗中液面下降的高度,则
是圆锥形漏斗中液面下降的高度,则 与下落时间
与下落时间 (分)的函数关系用图象表示只可能是( ).
(分)的函数关系用图象表示只可能是( ).
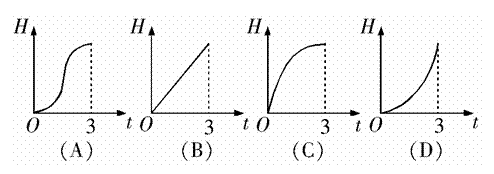
解析:由于圆柱中液面上升的速度是一个常量,所以 与
与 的关系不是(B)中所示,下落时间
的关系不是(B)中所示,下落时间 越大,液面下降的高度
越大,液面下降的高度 应越大,这种变化趋势应是越来越快,图象应当是下凸的,所以只可能是(D).
应越大,这种变化趋势应是越来越快,图象应当是下凸的,所以只可能是(D).
观察图形,借助图形来解决某些问题时,既要定性也要定量,仅画图示“意”是不够的,还必须反映出图形中相应的数量关系.
例2 问:圆 上到直线
上到直线 的距离为的点共有( ).
的距离为的点共有( ).
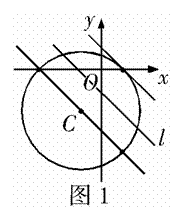 (A)1个 (B)2个 (C)3个 (D)4个
(A)1个 (B)2个 (C)3个 (D)4个
解析:到定直线 的距离为
的距离为 的点的轨迹是平行于
的点的轨迹是平行于 的两条直线.因此,问题就转化为判定这两条直线与已知圆的交点个数.
的两条直线.因此,问题就转化为判定这两条直线与已知圆的交点个数.
将圆 的方程变形为:
的方程变形为: ,知其圆心是
,知其圆心是 ,半径
,半径 ,而圆心到定直线
,而圆心到定直线 的距离为
的距离为 ,由此判定平行于直线
,由此判定平行于直线 且距离为
且距离为 的两条直线中,一条通过圆心
的两条直线中,一条通过圆心 ,另一条与圆
,另一条与圆 相切,所以这两条直线与圆
相切,所以这两条直线与圆 共有3个交点(如图1).故选(C).
共有3个交点(如图1).故选(C).
 注意:正确绘制图形,一定要注意把图形与计算结合起来,只有所画示意图准确,才能充分发挥图形的判定作用.
注意:正确绘制图形,一定要注意把图形与计算结合起来,只有所画示意图准确,才能充分发挥图形的判定作用.
观察是人们认识客观事物的开始,直观是图形的基本特征,观察图形的形状、大小和位置关系,并在此基础上揭示图形中蕴含的数量关系,是掌握数形结合思想的重要步骤.
例1 函数 的图象的一条对称轴方程是( ).
的图象的一条对称轴方程是( ).
(A) (B)
(B) (C)
(C) (D)
(D)
解析:对函数 的图象做深入的观察,可知,若直线
的图象做深入的观察,可知,若直线 通过这一曲线的一个最高点或最低点,则它必为曲线的一条对称轴.因此,解这个问题可以分别将
通过这一曲线的一个最高点或最低点,则它必为曲线的一条对称轴.因此,解这个问题可以分别将 代入函数的解析式,易得
代入函数的解析式,易得 时,
时, .故选(C).
.故选(C).
注意:要善于观察图形,发现基本性质.如本题若不能很好的掌握函数 的图象性质,而机械的画出函数
的图象性质,而机械的画出函数 的图象及其对称轴,虽然也可以做对,但却浪费了宝贵的时间.
的图象及其对称轴,虽然也可以做对,但却浪费了宝贵的时间.
例3 函数 ,满足
,满足 ,且
,且 ,则
,则 与
与 的大小关系是_____.
的大小关系是_____.
分析:先求 的值,再比较大小,要注意
的值,再比较大小,要注意 的取值是否在同一单调区间内.
的取值是否在同一单调区间内.
解:∵ ,∴函数
,∴函数 的对称轴是x=1.
的对称轴是x=1.
由此得 ,又由
,又由 =3,得 c=3.
=3,得 c=3.
∴函数 ,其在(-∞,1)上递减,在(1,+∞)上递增.
,其在(-∞,1)上递减,在(1,+∞)上递增.
若 ,则
,则 ≥
≥ ≥1,
≥1,
∴ .
.
若 ,则
,则 ,∴
,∴ .
.
综上可得 .
.
点评:比较大小的常用方法有:作差法、作商法、单调性法、中间量法等.
例4 函数 (
( ,且a≠1)在区间[-1,1]上有最大值14,则a的值是_____.
,且a≠1)在区间[-1,1]上有最大值14,则a的值是_____.
分析:令 可将问题转化成二次函数的最值问题,需注意换元后t的取值范围.
可将问题转化成二次函数的最值问题,需注意换元后t的取值范围.
解:令 ,则函数
,则函数 (
( ,且
,且 )可化为
)可化为 ,则对称轴为
,则对称轴为 ,
,
∴当 时,由
时,由 ,知
,知 ,即
,即 .
.
∴当 时,
时, .
.
解得  或
或 (舍去);
(舍去);
当 时,
时, ,
, ,即
,即 .
.
∴当 时,
时, .
.
解得  或
或 (舍去).
(舍去).
∴a的值是3或 .
.
点评:利用指数函数的单调性求最值时要注意方法的选取,比如:换元法,整体法等.
例2 已知函数 ,试证明函数
,试证明函数 是定义域内的增函数.
是定义域内的增函数.
分析:证明函数的单调性可用定义证明,也可用复合函数的单调性判断法则来考虑.
证明:由已知可得函数 的定义域是R,并且
的定义域是R,并且
 ,
,
设 ,且
,且 ,则
,则 ,
,
∵ 是R上的增函数,∴当
是R上的增函数,∴当 时,
时, .
.
又∵ ,
,
∴ ,即
,即 .
.
∴函数 是定义域内的增函数.
是定义域内的增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com