2、基本操作

(1)药品的取用

1药品取用的“六不”“两原则”：(1)‘‘六不”：不用手接触药品，不直接闻药品气味，不尝药品味道，对用剩的药品不放回原瓶，不随意丢弃，不拿出实验室(要放入指定的容器中)。(2)“两原则”：取药品时，如果没有说明药品用量，一般应按：固体只须盖满试管底部；液体取1 mL--2 mL。

2取用药品的方法：(1)固体药品的取用：取用粉末状或小颗粒固体药品用药匙或纸槽，步骤：“一斜二送三直立”；取用块状或大颗粒药品用镊子夹取，步骤：“一横二放三慢竖”。 (2)液体药品的取用方法：较多量时用倾倒法，瓶塞倒放，标签向着手心，瓶口紧挨容器口l。取用量少时，用胶头滴管。

(2)酒精灯的使用

使用酒精灯时：①酒精量不超过容器的2／3，也不少于1／3；②不可用燃着的酒精灯去点燃另一盏酒精灯；③酒精灯用完立即用灯帽盖灭，切不可用嘴吹灭；④加热玻璃仪器勿与灯芯接触，要用外焰加热。

(3)物质的加热

1固体的加热：固体试剂常常可以直接加热，盛固体试剂直接加热的仪器有试管、蒸发皿、燃烧匙等。

2液体的加热：(1)盛液体的试管可直接在火焰(外焰)上加热；试管夹夹在离试管口的1／3处；试管内液体的体积不超过试管容积的1／3；试管倾斜，试管口向上且与桌面成45°；管口不能对着有人的方向；先移动试管(或酒精灯)均匀

受热，后集中加热液体的中上部，再慢慢下移加热

(4)托盘天平的使用

称量时，应在两边托盘上放一张质量相同的称量纸，易潮解的药品要放在玻璃器皿中称量；称量前，将游码拨到标尺的“零”处，调节天平平衡；称量时左盘放称量物，右盘放砝码。

(5)量筒的使用

量筒的使用要注意以下几点：1不能加热；2不能用作反应容器；3根据量取液体体积的多少，选择合适的量筒；4读数时，量筒必须放平，视线与液体凹液面的最低处保持水平。

(6)过滤

1仪器：铁架台(带铁圈)、玻璃棒、烧杯、漏斗。

　　 2操作要求：操作时要做到“一贴二低三靠”。

　　 一贴：滤纸的折叠必须和漏斗的角度相符，使滤纸紧贴漏斗内壁，中间不留气泡。

　　 二低：滤纸的边缘须低于漏斗口约5 mm，漏斗内液面略低于滤纸边缘，以防固体混入滤液。

三靠：倒液时，盛装待过滤液体的烧杯嘴和玻璃棒相靠；液体沿玻璃棒流进过滤器，玻璃棒末端和滤纸三层部分相靠；漏斗下端的管口与用来装盛滤液的烧杯内壁相靠；使过滤后的清液成细流，沿漏斗颈和烧杯内壁流人烧杯中。

(7)药品的存放

1广口瓶--固体；细口瓶--液体；集气瓶--气体(密度比空气大，正放；密度比空气小，倒放)。

2遇光、受热易分解的药品用棕色瓶盛(如硝酸、硝酸银溶液)；盛碱溶液的试剂瓶应用橡皮塞。

3白磷存放在水中。

4浓硫酸、浓盐酸、浓硝酸、氢氧化钠、氢氧化钙、某些结晶水合物及有毒的化学试剂要密封后妥善保存。

5易燃物、易爆物要远离火源。

(8)实验安全及处置方法

1浓酸流到实验台上：加NaHCO₃溶液--水冲洗--抹布擦干。沾在皮肤或衣服上：应先用布拭去，再用大量水冲洗，最后涂上3%．5%的NaHCO₃溶液。

2浓碱流到实验台上：加稀醋酸--水冲洗--抹布擦干。沾到皮肤或衣服上：大量水冲洗--涂硼酸溶液。

[例1](2009·泰安)正确的化学实验操作对实验结果、人身安全非常重要。下图中的实验操作正确的是(　 )

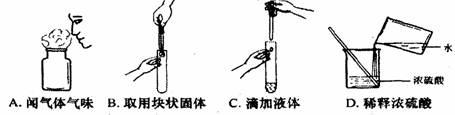
[答案]C

[解析]不能直接闻药品的味道，取用块状固体时，先要把试管横放，放在固体打碎试管底部，稀释浓硫酸时，应把浓硫酸往水里倒。

[规律小结]每个实验基本操作，都有对应的要求及注意事项，操作时一定要严格按照规定，防止发生意外。

变式训练一

1、常用仪器

(1)计量仪器--托盘天平、量筒、胶头滴管。①托盘天平。称量时：左物右码。加砝码：由大到小。精确度：0．1 g。②量筒，用于量取一定体积的液体药品。③胶头滴管，用于吸取和滴加少量液体。

(2)用于加热的仪器。①能在火焰上直接加热的仪器有试管、燃烧匙、蒸发皿、坩埚等；②须垫石棉网间接加热的仪器有烧杯、烧瓶、锥形瓶。

(3)加热器皿--酒精灯、石棉网。

8、已知在函数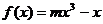的图象上以N(1，n)为切点的切线的倾斜角为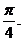

　 (Ⅰ)求m、n的值；

　 (Ⅱ)是否存在最小的正整数k，使得不等式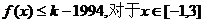恒成立？如果存在，请求出最小的正整数k；如果不存在，请说明理由；

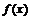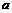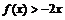7、已知二次函数的二次项系数为，且不等式的解集为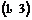　

⑴若方程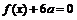有两个相等的实数根，求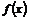的解析式；

⑵若函数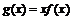无极值，求实数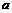的取值范围

6、已知函数．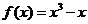

(1)求曲线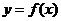在点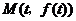处的切线方程；

(2)设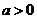，如果过点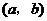可作曲线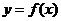的三条切线，证明：．

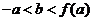5、已知函数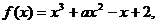

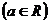
(1)若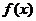在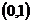上是减函数，求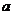的最大值；

(2)若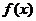的单调递减区间是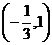，求函数y=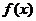图像过点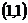的切线与两坐标轴围成图形的面积。

4、已知定义在R上的函数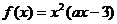，其中a为常数.

　 (I)若x=1是函数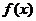的一个极值点，求a的值；

　 (II)若函数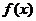在区间(－1，0)上是增函数，求a的取值范围；

　 (III)若函数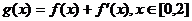，在x=0处取得最大值，求正数a的取值范围.

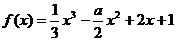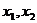3、已知函数且是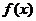的两个极值点，，

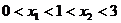(1)求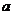的取值范围；

(2)若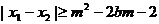，对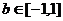恒成立。求实数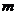的取值范围；

2、已知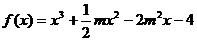(m为常数，且m>0)有极大值，

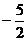(Ⅰ)求m的值；(Ⅱ)求曲线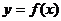的斜率为2的切线方程．

1、设函数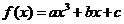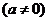为奇函数，其图象在点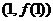处的切线与直线 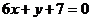平行，导函数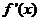的最小值为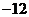 　

(Ⅰ)求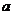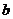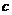，，的值；

(Ⅱ)求函数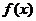的单调递增区间，并求函数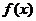在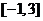上的最大值和最小值