
3、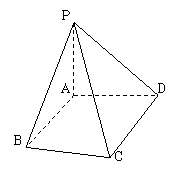 解:(1)M为PC的中点,设PD中点为N,
解:(1)M为PC的中点,设PD中点为N,
则MN=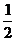 CD,且MN//
CD,且MN//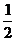 CD,∴MN=AB,MN//AB
CD,∴MN=AB,MN//AB
∴ABMN为平行四边形,∴BM//AN,
又PA=AD,∠PAD=900 ∴AN⊥PD,
又CD⊥AN,∴AN⊥面PCD,∴BM⊥面PCD,
(1) 延长CB交DA于E,
∵AB=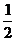 CD。AB//
CD。AB//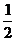 CD∴AE=AD=PA,∴PD⊥PE
CD∴AE=AD=PA,∴PD⊥PE
又∴PE⊥CD,∴PE⊥面PCD,
∴∠CPD为二面角C-PE-D的平面角;PD=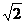 AD,CD=2AD;∴tan∠CPD=
AD,CD=2AD;∴tan∠CPD=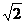
3、如图,已知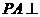 面
面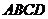 ,
,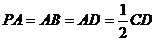 ,
,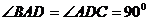 ;
;
(1)在面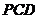 上找一点M,使
上找一点M,使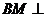 面
面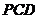 。
。
(2)求由面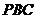 与面
与面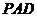 所成角的二面角的正切
所成角的二面角的正切
2、解:(Ⅰ)证明:在Rt△ABC中,∠C=30°,D为AC的中点,则△ABD是等边三角形
又E是BD的中点,∵BD⊥AE,BD⊥EF,折起后,AE∩EF=E,∴BD⊥面AEF
∵BD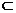 面BCD,∴面AEF⊥面BCD
面BCD,∴面AEF⊥面BCD
(Ⅱ)解:过A作AP⊥面BCD于P,则P在FE的延长线上,设BP与CD相交于Q,
令AB=1,则△ABD是边长为1的等边三角形,若AB⊥CD,则BQ⊥CD
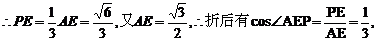
由于∠AEF=θ就是二面角A-BD-C的平面角,
2、在Rt△ABC中,∠ACB=30°,∠B=90°,D为AC中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角A-BD-C大小记为θ.
 (Ⅰ)求证:面AEF⊥面BCD;
(Ⅰ)求证:面AEF⊥面BCD;
(Ⅱ)θ为何值时,AB⊥CD.
1、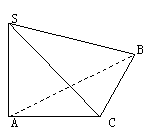 解:(1)∵∠SAB=∠SCA=900
解:(1)∵∠SAB=∠SCA=900
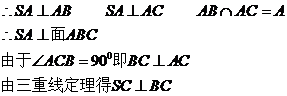
(2)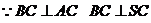
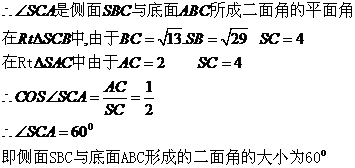
(3)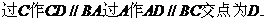
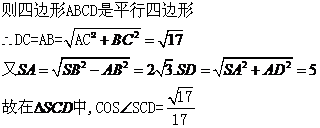

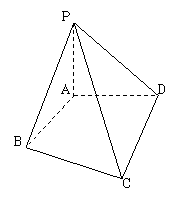
1、如图在三棱锥S 中
中 ,
,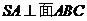 ,
,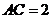 ,
,
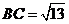 ,
,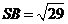 。
。
(1)证明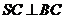 。(2)求侧面
。(2)求侧面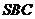 与底面
与底面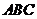 所成二面角的大小。
所成二面角的大小。
(3)求异面直线SC与AB所成角的大小。
13、解:(I)设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为
(1,5),(2,4),(3,3),(4,2),(5,1),共5个.……………………2分
又甲、乙二人取出的数字共有5×5=25(个)等可能的结果,
所以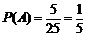 . …………6分
. …………6分
答:编号的和为6的概率为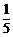 .…………………………………………………………………7分
.…………………………………………………………………7分
(Ⅱ)这种游戏规则不公平.……………………………………………………………………9分
设“甲胜”为事件B,“乙胜”为事件C, ……………………………………………10分
则甲胜即两数字之和为偶数所包含的基本事件数为13个:
(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),
(4,2) ,(4,4),(5,1) ,(5,3),(5,5).
所以甲胜的概率P(B)=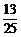 ,从而乙胜的概率P(C)=1-
,从而乙胜的概率P(C)=1-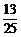 =
=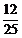 .…………14分
.…………14分
由于P(B)≠P(C),所以这种游戏规则不公平. ………………………………15分
13、口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.
12、解:(1)记“队员甲在三次游戏中,第一枪至少有一次命中”为事件A.
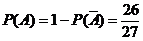 ……………………………………………………………………(5分)
……………………………………………………………………(5分)
(2)记在一次游戏中“第i次击中飞碟”为事件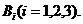
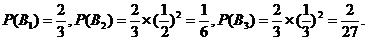 …………………………(8分)
…………………………(8分)
又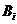 是相互独立事件.
是相互独立事件.
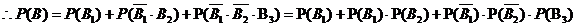
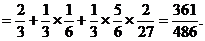 ………………………………………………………(12分)
………………………………………………………(12分)
12、国家射击队为备战2008年北京奥运会进行紧张艰苦的训练,训练项目完成后,教练总会设计安排一些放松、娱乐性恢复活动。在一次速射“飞碟”的游戏活动中,教练制定如下规则:每次飞碟飞行过程中只允许射击三次,根据飞碟飞行的规律,队员甲在飞行距离为50米远处命中的概率为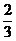 .
.
(1)如果队员甲一共参加了三次射击飞碟的游戏,试求队员甲在这三次游戏中第一枪至少有一次击中的概率。
(2)如果队员甲射击飞行距离为50米远处的飞碟,如果第一次未命中,则进行第二次射击,同时第二次射击时飞碟行距离变为100米;如果第二次未命中,则进行第三次射击,第三次射击时飞碟飞行距离变为150米(此后飞碟不在射程之内).已知,命中的概率与飞碟飞行距离的平方成反比.求队员甲在一次游戏中命中飞碟的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com