
8、证明:(1)取PD中点Q, 连EQ , AQ , 则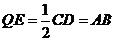 …1分
…1分
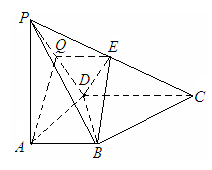
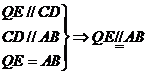 …………………………………………2分
…………………………………………2分
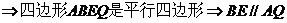 ………………3分
………………3分
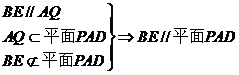 ………………………5分
………………………5分
 (2)
(2) 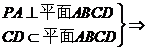
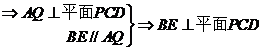 . …………………………10分
. …………………………10分
解:(3)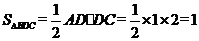 …………………………………11分
…………………………………11分
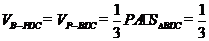 .
.
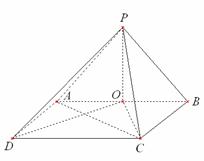
8、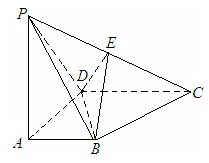 如图所示, 四棱锥P
如图所示, 四棱锥P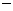 ABCD底面是直角梯形,
ABCD底面是直角梯形, 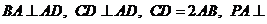 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明: 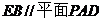 ;
;
(2)证明: 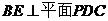 ;
;
(3)求三棱锥B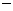 PDC的体积V.
PDC的体积V.
7、解法一:(Ⅰ)证明: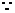 平面
平面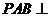 平面
平面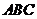 ,平面
,平面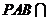 平面
平面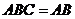 ,且
,且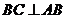 ,
,
 .
.
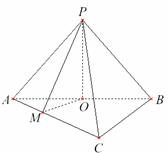
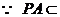 平面
平面 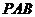 ,
, 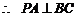 .
.
又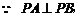
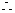
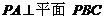 . ………4分
. ………4分
(Ⅱ)解:作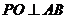 于点
于点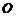 ,
,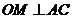 于点
于点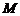 ,连结
,连结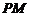 .
.
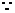 平面
平面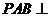 平面
平面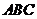 ,
, 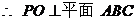 ,
,
根据三垂线定理得 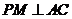 ,
,
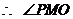 是二面角
是二面角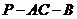 的平面角. ………….. 6分
的平面角. ………….. 6分
设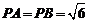 ,
, 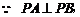
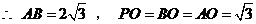 .
.
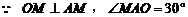 ,
, 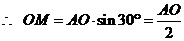 ,
,
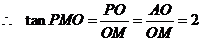 ,
………….. 8分
,
………….. 8分
即二面角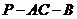 的大小是
的大小是 .
……….. 9分
.
……….. 9分
(Ⅲ)解:在底面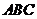 内分别过
内分别过 作
作 的平行线,交于点
的平行线,交于点 ,
,
 连结
连结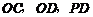 .
.
则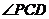 是异面直线
是异面直线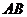 和
和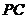 所成的角或其补角. ….. 11分
所成的角或其补角. ….. 11分
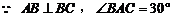 ,
,
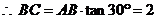 ,
, 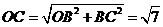 ,
,
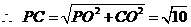 .
.
易知底面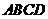 为矩形,从而
为矩形,从而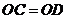 ,
,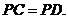
在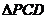 中,
中,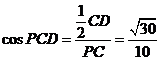 ,
………….. 13分
,
………….. 13分
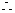 异面直线
异面直线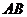 和
和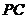 所成角的大小为
所成角的大小为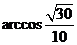 .
………….. 14分
.
………….. 14分
解法二: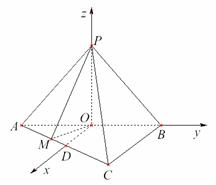 作
作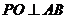 于点
于点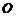 ,
,
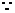 平面
平面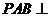 平面
平面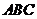 ,
,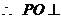 平面
平面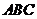 .
.
过点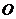 作
作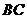 的平行线,交
的平行线,交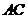 于点
于点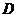 .
.
如图,以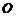 为原点,直线
为原点,直线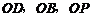 分别为
分别为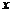 轴,
轴,
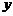 轴,
轴,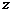 轴,建立空间直角坐标系 . …………..
2分
轴,建立空间直角坐标系 . …………..
2分
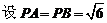 .
. 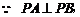
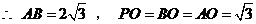 .
.
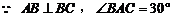 ,
,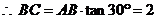 .
.
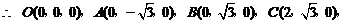
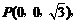
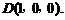 ………….. 4分
………….. 4分
(Ⅰ)证明: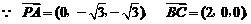
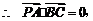
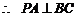 . 又
. 又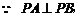
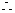
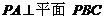 .
………….. 7分
.
………….. 7分
(Ⅱ)解:作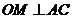 于点
于点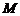 ,连结
,连结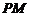 .
.
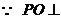 平面
平面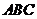 , 根据三垂线定理得
, 根据三垂线定理得 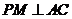 ,
,
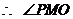 是二面角
是二面角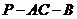 的平面角.
………….. 8分
的平面角.
………….. 8分
在 中,
中, 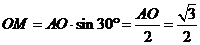 ,
,
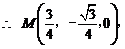 从而
从而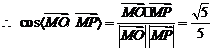 , …………..
10分
, …………..
10分
即二面角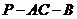 的大小是
的大小是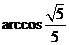 .
………….. 11分
.
………….. 11分
(Ⅲ)解: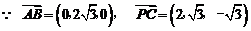 ,
,
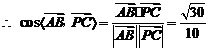 ,
,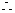 异面直线
异面直线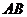 和
和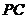 所成角的大小为
所成角的大小为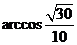 .
.
7、如图,在三棱锥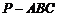 中,
中,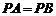 ,
,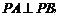
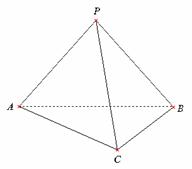
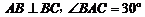 ,平面
,平面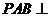 平面
平面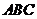 .
.
(Ⅰ)求证: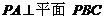 ;
;
(Ⅱ)求二面角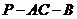 的大小;
的大小;
(Ⅲ)求异面直线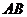 和
和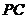 所成角的大小.
所成角的大小.
6、
 解法二:
解法二:
(1)解:同解法一………………5分
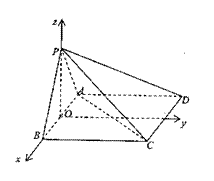
(2)解:建立如图的空间直角坐标系O-xyz,
则A(-1,0,0),B(1,0,0),
则P(0,0,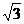 ),C(1,2,0)
),C(1,2,0)
设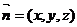 为平面PAC的一个法向量,
为平面PAC的一个法向量,
则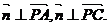
又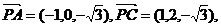
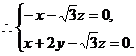 令z=1,得
令z=1,得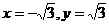 得
得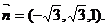
又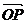 是平面ABC的一个法向量,设二面角B-AC-P的大小为
是平面ABC的一个法向量,设二面角B-AC-P的大小为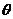 ,
,
则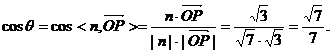
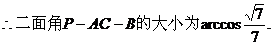 ………………10分
………………10分
(2) 解:设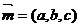 为平面PCD的一个法向量.
为平面PCD的一个法向量.
则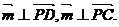 由D(-1,2,0),可知
由D(-1,2,0),可知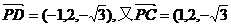 ),
),
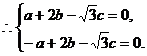 可得a=0,令
可得a=0,令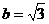 ,则c=2.得
,则c=2.得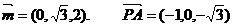 ,
,
设点A到平面PCD的距离为d,则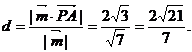
∴点A到平面PCD的距离为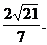
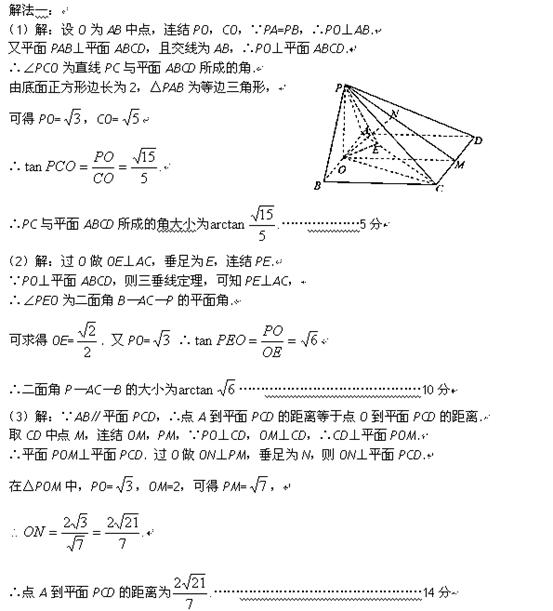
6、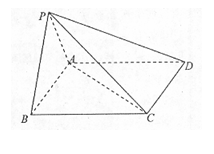 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形.(1)求PC与平面ABCD所成角的大小;
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,底面ABCD是边长为2的正方形,△PAB为等边三角形.(1)求PC与平面ABCD所成角的大小;
(2)求二面角B-AC-P的大小;
(3)求点A到平面PCD的距离.
5、方法一:(1)证明: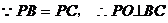
又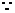 平面
平面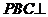 平面ABCD
平面ABCD
平面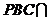 平面ABCD=BC,
平面ABCD=BC,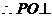 平面ABCD ……2分
平面ABCD ……2分
在梯形ABCD中,可得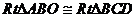
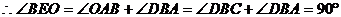 ,即
,即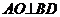
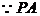 在平面ABCD内的射影为AO,
在平面ABCD内的射影为AO,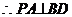 ……4分
……4分
(2)解: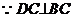 ,且平面
,且平面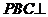 平面ABCD
平面ABCD
∴DC⊥平面PBC
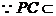 平面PBC,
平面PBC,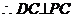
∴∠PCB为二面角P-DC-B的平面角 ……6分
 ∵△PBC是等边三角形,∴∠PCB=60°,即二面角P-DC-B的大小为60° ……8分
∵△PBC是等边三角形,∴∠PCB=60°,即二面角P-DC-B的大小为60° ……8分
(3)证明:取PB的中点N,连结CN
∵PC=BC,∴CN⊥PB ①
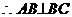 ,且平面
,且平面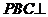 平面ABCD
平面ABCD
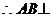 平面PBC ……………10分
平面PBC ……………10分
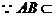 平面PAB
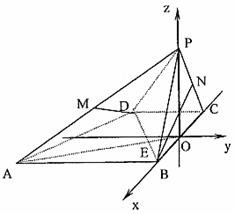
平面PAB 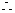 平面
平面 平面PAB ②
平面PAB ②
由①、②知CN⊥平面PAB
连结DM、MN,则由MN∥AB∥CD
MN=AB=CD,得四边形MNCD为平行四边形
 ∴CN∥DM ∴DM⊥平面PAB
∴CN∥DM ∴DM⊥平面PAB
∵DMÌ平面PAD 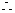 平面PAD⊥平面PAB ………………12分
平面PAD⊥平面PAB ………………12分
方法二:取BC的中点O,因为△PBC是等边三角形,
由侧面PBC⊥底面ABCD 得PO⊥底面ABCD ……1分
以BC中点O为原点,以BC所在直线为x轴,过点O与
AB平行的直线为y轴,建立如图所示的空间直角坐标系
O-xyz……2分
(1)证明:∵CD=1,则在直角梯形中,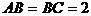
在等边三角形PBC中,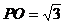
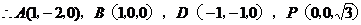
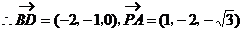
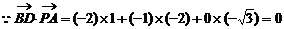
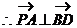 ,即
,即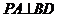 ……4分
……4分
(2)解:取PC中点N,则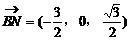
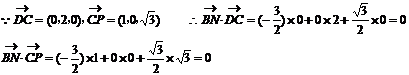
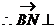 平面PDC,显然
平面PDC,显然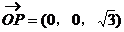 ,且
,且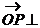 平面ABCD
平面ABCD
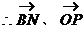 所夹角等于所求二面角的平面角 ……6分
所夹角等于所求二面角的平面角 ……6分
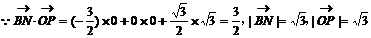
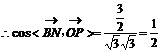
 二面角
二面角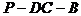 的大小为
的大小为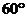 ……8分
……8分
(3)证明:取PA的中点M,连结DM,则M的坐标为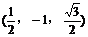
又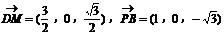 ……10分
……10分
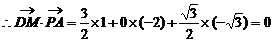
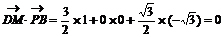
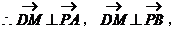 即
即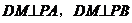
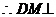 平面PAB,
平面PAB,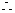 平面
平面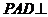 平面PAB.
平面PAB.
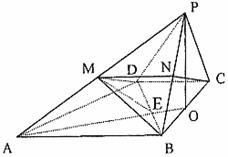
5、如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,
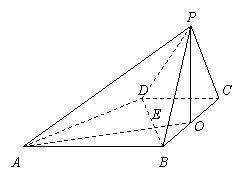 AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E.
AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P-DC-B的大小;
(3)求证:平面PAD⊥平面PAB.
4、解:(I)因为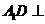 平面
平面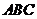 ,
,
所以平面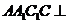 平面
平面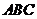 ,
,
 又
又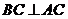 ,所以
,所以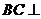 平面
平面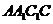 ,
,
得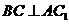 ,又
,又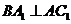
所以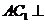 平面
平面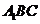 ;……………4分
;……………4分
(II)因为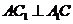 ,所以四边形
,所以四边形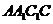 为 菱形,
为 菱形,
故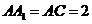 ,又
,又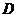 为
为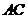 中点,知
中点,知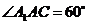 。
。
取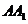 中点
中点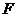 ,则
,则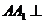 平面
平面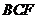 ,从而面
,从而面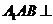 面
面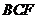 ,
,
过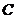 作
作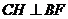 于
于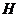 ,则
,则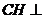 面
面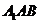 ,
,
在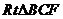 中,
中,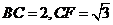 ,故
,故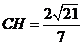 ,即
,即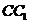 到平面
到平面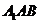 的距离为
的距离为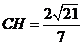 。
。
(III)过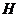 作
作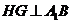 于
于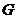 ,连
,连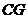 ,则
,则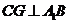 ,
,
从而 为二面角
为二面角 的平面角,
的平面角,
 在
在 中,
中,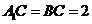 ,所以
,所以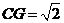 ,在
,在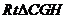 中,
中,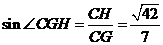 ,
,
故二面角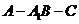 的大小为
的大小为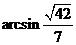 。……………12分
。……………12分
解法2:(I)如图,取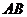 的中点
的中点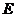 ,则
,则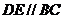 ,因为
,因为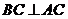 ,
,
所以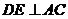 ,又
,又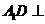 平面
平面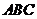 ,
,
以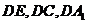 为
为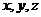 轴建立空间坐标系,
轴建立空间坐标系,
则 ,
,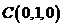 ,
,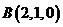 ,
,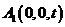 ,
,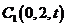 ,
,
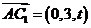 ,
,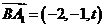 ,
,
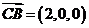 ,由
,由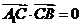 ,知
,知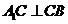 ,
,
又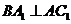 ,从而
,从而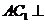 平面
平面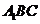 ;……………4分
;……………4分
(II)由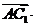
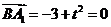 ,得
,得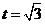 。
。
设平面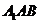 的法向量为
的法向量为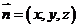 ,
,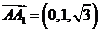 ,
,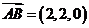 ,所以
,所以
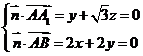 ,设
,设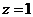 ,则
,则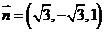
所以点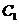 到平面
到平面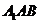 的距离
的距离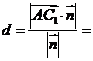
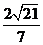 。……………8分
。……………8分
(III)再设平面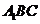 的法向量为
的法向量为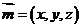 ,
,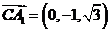 ,
,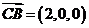 ,
,
所以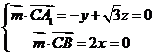 ,设
,设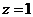 ,则
,则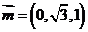 ,
,
故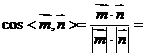
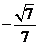 ,根据法向量的方向,可知二面角
,根据法向量的方向,可知二面角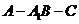 的大小为
的大小为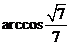 。
。
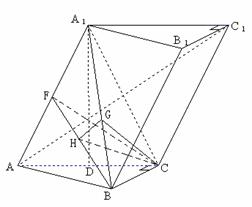
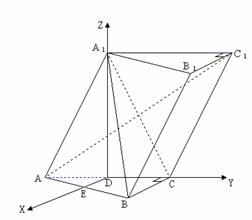
4、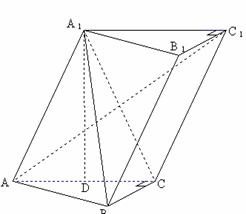 已知斜三棱柱
已知斜三棱柱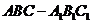 ,
,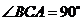 ,
,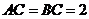 ,
,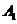 在底面
在底面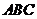 上的射影恰为
上的射影恰为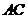 的中点
的中点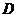 ,又知
,又知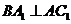 。
。
(I)求证: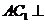 平面
平面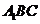 ;
;
(II)求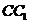 到平面
到平面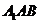 的距离;
的距离;
(III)求二面角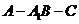 的大小。
的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com