
2、 [巩固]-1,[提高]在同一坐标系内画函数y=3-x,y=lgx,y=10x的图象,交点为A、B,A、B关于直线y=x对称,得x1=3-x2;3、 [巩固] g(x)= x2-ax+3a在区间[2,+∞ 上递增且g(x)= x2-ax+3a>0在区间[2,+∞
上递增且g(x)= x2-ax+3a>0在区间[2,+∞ 上恒成立,即a≤4且g(2)>0得-4<a≤4;
上恒成立,即a≤4且g(2)>0得-4<a≤4;
5.函数y= ,(
,( )的值域主要取决于g(x)。如:0<g(x)≤4,则
)的值域主要取决于g(x)。如:0<g(x)≤4,则 ∈[-2,+
∈[-2,+ ),其中0<g(x)只是保证对数值存在的,并不限制对数值的范围。若g(x)无最(极)大值(即上无界),则函数y=
),其中0<g(x)只是保证对数值存在的,并不限制对数值的范围。若g(x)无最(极)大值(即上无界),则函数y= ,(
,( )的值域为R
)的值域为R g(x)min≤0(特别地:当g(x)是二次项系数为正的二次函数时g(x)min≤0
g(x)min≤0(特别地:当g(x)是二次项系数为正的二次函数时g(x)min≤0 ⊿≥0); 函数y=
⊿≥0); 函数y= 有最值
有最值 g(x)min≥0。
g(x)min≥0。
[举例] 函数y=log (2x2-2x+1)的值域为
。
(2x2-2x+1)的值域为
。
解析:2x2-2x+1=2(x- )2+
)2+ ≥
≥ , log
, log (2x2-2x+1)≤1,∴函数值域为(-
(2x2-2x+1)≤1,∴函数值域为(- ,1
,1 。
。
[巩固] 设函数f(x)=lg(x2+ax-a-1),给出下列命题:①f(x)有最小值;②当a=0时,f(x)值域为R;③当a>0时,在[2,+∞ 上有反函数;④若f(x)在区间[2,+∞
上有反函数;④若f(x)在区间[2,+∞ 上单调递增,则实数a的取值范围是a≥-4.其中正确命题的序号是_____________
上单调递增,则实数a的取值范围是a≥-4.其中正确命题的序号是_____________
简答
4.函数y=ax的值域为(0,+ )。特别关注函数y=ax的值与1的大小,函数y=
)。特别关注函数y=ax的值与1的大小,函数y= 的值与0的大小。
的值与0的大小。
[举例1] 函数y= 的值域是( )
的值域是( )
(A)(- )
(B)(-
)
(B)(- 0)
0) (0,+
(0,+ )
)
(C)(-1,+ )
(D)(-
)
(D)(- ,-1)
,-1) (0,+
(0,+ )
)
解析:思路一:“逆求”: 得:
得: >0或
>0或 <-1,选D。思路二:
<-1,选D。思路二: ,“取倒数”要特别注意不等式两边同号,若-1<
,“取倒数”要特别注意不等式两边同号,若-1< <0,则
<0,则 <-1;若
<-1;若 >0,则
>0,则 >0,综上,选D。
>0,综上,选D。
[举例2] .若logm9<logn9<0,那么m,n满足的条件是( )
(A)m>n>1 (B)n>m>1 (C)0<n<m<1 (D)0<m<n<1
解析:logm9与logn9底数不同,比较大小不甚方便,注意到logm9= ,则由
,则由
logm9<logn9<0

 log9n<log9m<0
log9n<log9m<0 0<n<m<1,选C。
0<n<m<1,选C。
[巩固] 已知g(x)=loga (a>0且a
(a>0且a 1)在(-1,0)上有g(x)>0,则f(x)=a
1)在(-1,0)上有g(x)>0,则f(x)=a 是( )
是( )
(A)在(- ,0)上的增函数
(B)在(-
,0)上的增函数
(B)在(- ,0)上的减函数
,0)上的减函数
(C)在(- ,-1)上的增函数 (D)在(-
,-1)上的增函数 (D)在(- ,-1)上的减函数
,-1)上的减函数
3.关注对数函数的定义域,特别是在解对数不等式(留意对数变形的等价性)和研究对数函数的单调性(函数有意义才谈得上增减)时。
[举例1]函数f(x)的图像与函数g(x)=( )x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为( )
)x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为( )
(A)(0,1) (B)[1,+ ] (C)(-
] (C)(- ,1) (D)[1,2]
,1) (D)[1,2]
解析:f(x)与g(x)互为反函数,即f(x)= , f(2x-x2)=
, f(2x-x2)=  ,记h(x)=2x-x2,
,记h(x)=2x-x2,
则h(x)递增(“外层”递减)且h(x)>0(真数),∴x∈(0,1 ,故选A。(在函数定义域内区间的“开”“闭”不影响函数的单调性,所以求函数单调区间时一般用开区间比较“稳妥”)。
,故选A。(在函数定义域内区间的“开”“闭”不影响函数的单调性,所以求函数单调区间时一般用开区间比较“稳妥”)。
[举例2]已知命题p: ;命题q:
;命题q: >1;则命题p是命题q的: ( )
>1;则命题p是命题q的: ( )
A.充分不必要条件,B.必要不充分条件,
C.充要条件 D.既不必要也不充分条件
解析:命题p: ,移项通分得:
,移项通分得: ,“序轴标根”得:
,“序轴标根”得: ∈
∈ ,
,
命题q: >1等价于:
>1等价于: >2,即
>2,即 ∈
∈ (注意:不等式
(注意:不等式 >1与不等式:2
>1与不等式:2 >1不等价,
>1不等价, >1等价于2
>1等价于2 >1);从集合包含关系更容易看清两个命题的逻辑关系,选D。
>1);从集合包含关系更容易看清两个命题的逻辑关系,选D。
[巩固]已知函数f(x)=log2(x2-ax+3a)在区间[2,+∞ 上递增,则实数a的取值范围是 。
上递增,则实数a的取值范围是 。
2.指数函数y=ax与对数函数y= ,(
,( )是互为反函数即
)是互为反函数即 它是实现指数式与对数式相互转换的桥梁。当a>1时,两个函数在定义域内都递增;当0<a<1时,两个函数在定义域内都递减。
它是实现指数式与对数式相互转换的桥梁。当a>1时,两个函数在定义域内都递增;当0<a<1时,两个函数在定义域内都递减。
[举例1]光线透过一块玻璃板,其强度要减弱 ,要使光线的强度减弱到原来的
,要使光线的强度减弱到原来的 以下,至少需要这样的玻璃板 块。(参考数据:lg2=0.3010,lg3=0.4771)
以下,至少需要这样的玻璃板 块。(参考数据:lg2=0.3010,lg3=0.4771)
解析:记光线原来的强度为 ,透过一块玻璃板后其强度变为
,透过一块玻璃板后其强度变为
 ,透过
,透过 块玻璃板后其强度变为:
块玻璃板后其强度变为: ,则
,则 <
<
 ,即
,即 <
< ,
,
 (2lg3-1)<-lg3
(2lg3-1)<-lg3
 ≈10.4,(注意:2lg3-1<0),∴
≈10.4,(注意:2lg3-1<0),∴ =11.
=11.
[举例2] loga ,则a的取值范围是( )
,则a的取值范围是( )
(A)(0, )
) (1,+
(1,+ )
(B)(
)
(B)( ,+
,+ )
)
(C)( )
(D)(0,
)
(D)(0, )
) (
( ,+
,+ )
)
解析:若a>1,则 <a,∴a>1;若0<a<1,则
<a,∴a>1;若0<a<1,则 >a, ∴0<a<
>a, ∴0<a< ;综上,选A。(本题中视1为logaa是化“数”为“对数”的通法)。
;综上,选A。(本题中视1为logaa是化“数”为“对数”的通法)。
[巩固] 若 ,
, ,则
,则 =__________。
=__________。
[提高] 方程x+lgx=3,x+10x=3的解分别为x1,x2,则x1+x2=____________
1.指数函数、对数函数的运算性质。特别关注:axbx=(ab)x,(ax)y=axy,如:2x3x=6x,(2x)=4x等; ,(
,( ,
, );
); ,(
,( ,
, )
)
[举例]设f(x)=4x+4-x-(21+x+21-x)+2则f(x)的最小值为 ;
解析:记2x+2-x
=t,t≥2, 4x+4-x+2 =t2,g(t)= t2-2t=(t-1)2-1,
函数g(t)在[2,+
 上递增,
上递增,
∴g(t)min = g(2)=0,即f(x)的最小值为0;注意:此题如果使用基本不等式,有:4x+4-x ≥2,
21+x+21-x ≥4,则f(x)=4x+4-x-(21+x+21-x)+2≥2-4+2=0,看似巧妙,结果也正确,其实荒唐,因为上述过程的实质是“同向不等式相减”。
1. [巩固] 函数y=f(x)的图象关于x=2对称,得a=5,图示可得1<x≤2或-4≤x<-3。
[提高] 函数y=f(x)的周期为2,得f(x)在[0,1]上递增,又 +
+ <
< ,移项得sin
,移项得sin <cos
<cos ,选B;2、 [巩固]关注两段函数在x=1时的函数值的大小,得
,选B;2、 [巩固]关注两段函数在x=1时的函数值的大小,得 3. [巩固]D;
3. [巩固]D;
5.求参变量的取值范围通常采用分离参数法,转化为求某函数的值域或最值;也可以整体研究函数y=f(a,x)的最值。
[举例] 关于x的方程22x-m2x+4=0(x<0)有解,求实数m的取值范围。
解析:令2x=t,(0<t<1),原方程变为:t2-mt+4=0在(0,1)上有解,这里显然不能简单地用判别式处理,因为⊿≥0不能保证方程在(0,1)上有解,还需附加更多的条件才成,繁!
事实上,求参变量范围的问题首先考虑的是“分离参变量”: =
= ,所谓方程有解,即
,所谓方程有解,即 在函数
在函数 的值域内(这也是解决方程有解问题的通法),∵t∈(0,1),∴不能使用基本不等式(等号不成立),注意到函数
的值域内(这也是解决方程有解问题的通法),∵t∈(0,1),∴不能使用基本不等式(等号不成立),注意到函数 在(0,1)上递减,∴
在(0,1)上递减,∴ ∈(5,
∈(5, )即
)即 ∈(5,
∈(5, )。
)。
[迁移]若函数f(x)=loga(x2-ax+3),(a>0且a 1)满足:对任意x1,x2,当x1<x2
1)满足:对任意x1,x2,当x1<x2 时,f(x1)-f(x2)>0,则实数a的取值范围是
时,f(x1)-f(x2)>0,则实数a的取值范围是
A.(0,1)∪(1,3)
B.(1,3) C.
(0,1)∪(1, ) D. (1,
) D. (1, )
)
简答
4. 求最值的常用方法:①单调性:研究函数在给定区间内的单调情况是求函数值域的最重要也是最根本的方法。②基本不等式:满足条件“一正、二定、三相等”时方可使用,如果“不相等”,常用函数 的单调性解决。③逆求法:用y表示x,使关于x的方程有解的y的范围即为值域,常用于求分式函数的值域,判别式法就是其中的一种。
的单调性解决。③逆求法:用y表示x,使关于x的方程有解的y的范围即为值域,常用于求分式函数的值域,判别式法就是其中的一种。
④换元法:需要把一个式子看作一个整体即可实施换元,“三角换元”是针对“平方和 等于1”实施的,目的多为“降元”;求值域时的换元主要是为了“去根号”。⑤数形结合。
[举例1]已知函数 ,则其图象的最低点的坐标是
( )
,则其图象的最低点的坐标是
( )
A、(1,2) B、 C、(0,2) D、不存在
C、(0,2) D、不存在
解析:求函数图象的最低点的坐标即求函数当x取何值时函数取得最小值,最小值是多少;
此题不宜“逆求”(判别式法),因为⊿≥0不能保证x>-1(这是使用“判别式法”时需特别注意的)。记x+1=t,(t>0),此时x=t-1,设g(t)= (当且仅当t=1即x=0时等号成立,(注意这里的“换元”实质是“整体化”的具体落实,将需要“整体化”的部分换成一个变量,比“凑”更具一般性也更易实施),选C。
(当且仅当t=1即x=0时等号成立,(注意这里的“换元”实质是“整体化”的具体落实,将需要“整体化”的部分换成一个变量,比“凑”更具一般性也更易实施),选C。
[举例2]已知 +,则
+,则 的最小值为
的最小值为
解析:本题关注 的取值范围,对
的取值范围,对 使用基本不等式,当且仅当
使用基本不等式,当且仅当 =±1时等号成立,事实上:
=±1时等号成立,事实上: ,∴等号不成立,即不能使用基本不等式。记
,∴等号不成立,即不能使用基本不等式。记 =
=
(0< ≤
≤ ),
),  =
= +
+ =g(
=g( ),函数g(
),函数g( )在(0,
)在(0,
 上递减,∴g(
上递减,∴g( )min=g(
)min=g( )=
)= 。
。
3.研究方程根的个数、超越方程(不等式)的解(特别是含有参量的)、二次方程根的分布、二次函数的值域、三角函数的性质(包括值域)、含有绝对值的函数性质、已知函数值域研究定义域等一般用函数图象(作图要尽可能准确)。
[举例1]若在 内有两个不同的实数值满足等式
内有两个不同的实数值满足等式 则
则 的范围是
的范围是
|
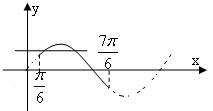 解析:
解析: =2sin(
=2sin( ),∵
),∵ ∈
∈ ,将
,将 视为一个角
视为一个角 ,
, ∈[
∈[ ,
, ],作函数
],作函数 在[
在[ ,
, ]上的图象(注意:无需作函数
]上的图象(注意:无需作函数 =2sin(
=2sin( )的图象),容易看出,当
)的图象),容易看出,当 =
= +1∈[1,2
+1∈[1,2 时,函数
时,函数 与函数
与函数 =
= +1的图象有两个交点,此时
+1的图象有两个交点,此时 ∈[0,1
∈[0,1 。
。
[举例2]不等式 的解集为[1,2),则a的值为
的解集为[1,2),则a的值为
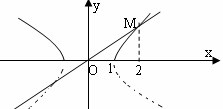 解析:分别作函数
解析:分别作函数 和函数
和函数
的图象如右,(函数 即
即 ,
,
 ,双曲线在x轴上方的部分)。
,双曲线在x轴上方的部分)。
两图象交于M点,要使不等式解集为[1,2),
则M(2, ),即
),即 。
。
[巩固]已知函数f(x)= 的定义域为[a,b],值域为[0,2],则a,b满足:
的定义域为[a,b],值域为[0,2],则a,b满足:
A.a= ,b=1或 a=1,b=4, B.a=
,b=1或 a=1,b=4, B.a= ,1≤b≤4,
,1≤b≤4,
C. ≤a≤1,b=4,
D. a=
≤a≤1,b=4,
D. a= ,1≤b≤4或
,1≤b≤4或 ≤a≤1,b=4。
≤a≤1,b=4。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com