
(2)当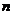 ≥1时,
≥1时,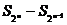 =(共2n-1项)
=(共2n-1项)
(1)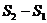 =,
=,
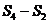 =,
=,
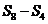 =。
…………2分
=。
…………2分
16. 已知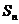 是数列{
是数列{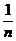 }的前
}的前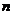 项和,
项和,
(1)分别计算 的值;
的值;
(2)证明:当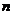 ≥1时,
≥1时,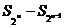 ≥,并指出等号成立条件;
≥,并指出等号成立条件;
(3)利用(2)的结论,找出一个适当的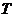 ∈N,使得
∈N,使得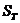 >2008;
>2008;
(4)是否存在关于正整数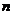 的函数
的函数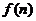 ,使得
,使得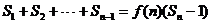 对于大于1的正整数
对于大于1的正整数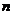 都成立?证明你的结论。
都成立?证明你的结论。
【标准答案】
即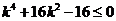 ,解得
,解得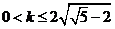 .(14分)
.(14分)
说明:二元不等式求最值这是考试大纲的要求,不等式恒成立变形转化为函数值之间的关系,变形换元化归基本的初等函数的复合函数,构造函数的单调性解决,这是函数的一个重要应用,考查了正比例和反比例函数的性质,最后一问的恒成立问题换元后,分离参数化归对号函数单调性解决值域,再构建不等式解参数范围,这是高考命题的热点。
要使函数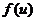 在
在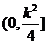 上恒有
上恒有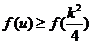 ,必有
,必有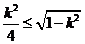 ,
,
因此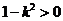 ,∴函数
,∴函数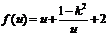 在
在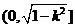 上递减,在
上递减,在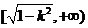 上递增,
上递增,
由(II)知,要使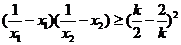 对任意
对任意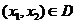 恒成立,必有
恒成立,必有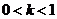 ,
,
即求使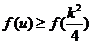 对
对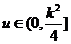 恒成立的
恒成立的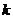 的范围.(10分)
的范围.(10分)
(III)令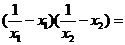
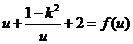 ,则
,则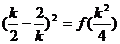 ,
,
即当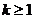 时不等式
时不等式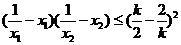 成立. (9分)
成立. (9分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com