21. (本题满分13分) 　　已知数列中，点在函数的图像上，(1)求，(2)若，求 　　　　　

(2).　　　

20. (本题满分13分)某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本(万元)与年产量吨之间的关系式可以近似地表示为，已知此生产线年产量最大为210吨。

(1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；

(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

解：(1)每吨平均成本为(万元)

则 。当且仅当，即时取等号

所以年产量为200吨时，每吨平均成本最低为32万元。

(2)设年获得总利润为万元

则

　 因为在上是增函数，所有时有最大值为。

所以年产量为210吨时，可以获得最大利润1660万元。

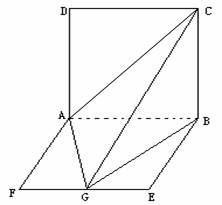
18. (本题满分12分)．如图:平面平面,是正方形,矩形，且,是的中点。

(1)求证平面平面;(2)求四面体的体积。

　　　　　　　　　　　　　　　　　　　　　　　　　 ，

(1)证明：因为是正方形,矩形，且,是的中点。

得：于是有所以,又因为

平面平面，且,所以,得,所以平面.　　 又因为直线在平面内，故：平面平面.

(2)由(1)知：直线平面,所以是四面体的高,而:

,所以

.19. (本题满分13分)　 已知函数

(1)当时，求函数的单调递增区间；

(2)当时，函数的值域是，求的值

解：

(1)当时，

当时，是增函数，

所以，函数的单调递增区间为

(2)当时，在时，函数取得最小值3，即①

在时，函数取得最大值4，即-，②

由 ①+②得

16 (本题满分12分)已知点M在X轴上，点N在Y轴上，且,点P为线段MN的中点。　　　　

(1) 求点P的轨迹方程。

(2)若直线与上述轨迹交于A.B两点，且,求：的值。

解：(1)连,因为为直角三角形斜边的中点，所以，所以,点P的轨迹方程：

。

(2)因为直线与交于A.B两点，且所以

=

17. (本题满分12分)中心在原点的椭圆与抛物线有一个公共焦点，且其离心率是双曲线的离心率的倒数，

(1)求椭圆方程。

(2)若(1，)是直线被椭圆截得的线段的中点，求直线的方程。

解：(1)由条件知：椭圆的焦点且他的离心率为，知

所以椭圆为：　

(2)设线段AB的则B。由

及，两式相减得直线的方程为

15.已知是1+2与1-2的等比中项，则的最大值为

解：由条件得当取最大值时，所以

所以

14.数学拓展课上，老师定义了一种运算“”，对与满足以下运算性质：①22=1，②,则用含n的代数式表示为_______________

先考察一下事件：

　　　　 ，

　　　　　 可见

13.过点和双曲线右焦点的直线方程为　　　　　　　　 　　　.

答案：

解析： ，故，双曲线的右焦点为.

，故直线的方程为，即.

12.已知.若，则与夹角的大小为　　　　　　 .

答案：

解析：，又因为，所以.

11．已知一种原料的最佳加入量在1000到2000之间。若按照0.618法优选，则第二次试点加入量为

解：

10.函数的最小正周期　　　　　 .

答案：

解析：　 最小正周期.