
47.(08四川泸州)(本题答案暂缺)四(本大题 10分)
46.(08四川凉山)25.(9分)如图,在 中
中 ,
, 是
是 的中点,以
的中点,以 为直径的
为直径的 交
交 的三边,交点分别是
的三边,交点分别是 点.
点. 的交点为
的交点为 ,且
,且 ,
, .
.
(1)求证: .
.
(2)求 的直径
的直径 的长.
的长.
 (3)若
(3)若 ,以
,以 为坐标原点,
为坐标原点, 所在的直线分别为
所在的直线分别为 轴和
轴和 轴,建立平面直角坐标系,求直线
轴,建立平面直角坐标系,求直线 的函数表达式.
的函数表达式.
(08四川凉山25题解析)25.(9分)
(1)连接
 是圆直径,
是圆直径, ,即
,即
 ,
, .················································································· 1分
.················································································· 1分
 .
. 在
在 中
中 ,
, .··························· 2分
.··························· 2分
(2) 是
是 斜边
斜边 的中点,
的中点, ,
, ,
,
又由(1)知 ,
, .
.
又 ,
, 与
与 相似······················································ 3分
相似······················································ 3分

 ············································································ 4分
············································································ 4分
又 ,
,
 ,
, ,
, ······································ 5分
······································ 5分
设 ,
, ,
, ,
,
 直径
直径 .······························································································· 6分
.······························································································· 6分
(3) 斜边上中线
斜边上中线 ,
,

 在
在 中
中 ,
, ,
, ······························ 7分
······························ 7分
设直线 的函数表达式为
的函数表达式为 ,
,
根据题意得 ,
,
 解得
解得
 直线
直线 的函数解析式为
的函数解析式为 (其他方法参照评分)································· 9分
(其他方法参照评分)································· 9分
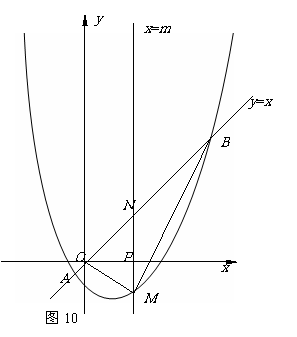
25.如图10,已知抛物线 经过点(1,-5)和(-2,4)
经过点(1,-5)和(-2,4)
(1)求这条抛物线的解析式.
(2)设此抛物线与直线 相交于点A,B(点B在点A的右侧),平行于
相交于点A,B(点B在点A的右侧),平行于 轴的直线
轴的直线 与抛物线交于点M,与直线
与抛物线交于点M,与直线 交于点N,交
交于点N,交 轴于点P,求线段MN的长(用含
轴于点P,求线段MN的长(用含 的代数式表示).
的代数式表示).
(3)在条件(2)的情况下,连接OM、BM,是否存在 的值,使△BOM的面积S最大?若存在,请求出
的值,使△BOM的面积S最大?若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
43.(08四川广安)(本题答案暂缺)七、解答题(本大题满分12分)
28. 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且 =3
=3 ,sin∠OAB=
,sin∠OAB= .
.
(1)若点C是点B关于x轴的对称点,求经过O、C、A三点的抛物线的函数表达式;
(2)在(1)中,抛物线上是否存在一点P,使以P、O、C、A为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若将点O、点A分别变换为点Q( -2k ,0)、点R(5k,0)(k>1的常数),设过Q、R两点,且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N,其顶点为M,记△QNM的面积为 ,△QNR的面积
,△QNR的面积 ,求
,求 ∶
∶ 的值.
的值.
42.(08四川成都)(本题答案暂缺)四、(共12分)
39.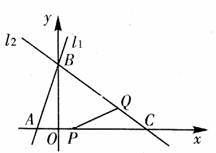 (08山西省卷)(本题答案暂缺)26.(本题14分)如图,已知直线
(08山西省卷)(本题答案暂缺)26.(本题14分)如图,已知直线 的解析式为
的解析式为 ,直线
,直线 与x轴、y轴分别相交于A、B两点,直线
与x轴、y轴分别相交于A、B两点,直线 经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线
经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线 从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(
从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒( )。
)。
(1)求直线 的解析式。
的解析式。
(2)设△PCQ的面积为S,请求出S关于t的函数关系式。
(3)试探究:当t为何值时,△PCQ为等腰三角形?
40(08山西太原)29.(本小题满分12分)
如图,在平面直角坐标系 中,直线
中,直线 与
与 交于点
交于点 ,分别交
,分别交 轴于点
轴于点 和点
和点 ,点
,点 是直线
是直线 上的一个动点.
上的一个动点.
(1)求点 的坐标.
的坐标.
(2)当 为等腰三角形时,求点
为等腰三角形时,求点 的坐标.
的坐标.
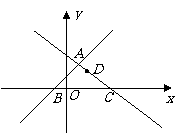 (3)在直线
(3)在直线 上是否存在点
上是否存在点 ,使得以点
,使得以点 为顶点的四边形是平行四边形?如果存在,直线写出
为顶点的四边形是平行四边形?如果存在,直线写出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(08山西太原29题解析)29.解:(1)在 中,当
中,当 时,
时, ,
,
 ,点
,点 的坐标为
的坐标为 .·········································································· 1分
.·········································································· 1分
在 中,当
中,当 时,
时, ,点
,点 的坐标为(4,0).·· 2分
的坐标为(4,0).·· 2分
由题意,得 解得
解得
 点
点 的坐标为
的坐标为 .····················································································· 3分
.····················································································· 3分
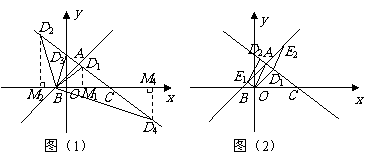 (2)当
(2)当 为等腰三角形时,有以下三种情况,如图(1).设动点
为等腰三角形时,有以下三种情况,如图(1).设动点 的坐标为
的坐标为 .
.
由(1),得 ,
, .
.
①当 时,过点
时,过点 作
作 轴,垂足为点
轴,垂足为点 ,则
,则 .
.
 .
.
 ,点
,点 的坐标为
的坐标为 .················································· 4分
.················································· 4分
②当 时,过点
时,过点 作
作 轴,垂足为点
轴,垂足为点 ,则
,则 .
.
 ,
, ,
,
 .
.
解,得 (舍去).此时,
(舍去).此时, .
.
 点
点 的坐标为
的坐标为 .·············································································· 6分
.·············································································· 6分
③当 ,或
,或 时,同理可得
时,同理可得 .····················· 9分
.····················· 9分
由此可得点 的坐标分别为
的坐标分别为 .
.
评分说明:符合条件的点有4个,正确求出1个点的坐标得1分,2个点的坐标得3分,3个点的坐标得5分,4个点的坐标得满分;与所求点的顺序无关.
(3)存在.以点 为顶点的四边形是平行四边形有以下三种情形,如图(2).
为顶点的四边形是平行四边形有以下三种情形,如图(2).
①当四边形 为平行四边形时,
为平行四边形时, .··········································· 10分
.··········································· 10分
②当四边形 为平行四边形时,
为平行四边形时, .············································ 11分
.············································ 11分
③当四边形 为平行四边形时,
为平行四边形时, .········································ 12分
.········································ 12分
41(08陕西省卷)25、(本题满分12分)
某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
如图,甲、乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学。点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的 km处。
km处。
为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:
方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值。
综上,你认为把供水站建在何处,所需铺设的管道最短?

(08陕西省卷25题解析)25、解:方案一:由题意可得:MB⊥OB,
∴点M到甲村的最短距离为MB。…………………(1分)
∵点M到乙村的最短距离为MD,
∴将供水站建在点M处时,管道沿MD、MB线路铺设的长度之和最小,
即最小值为MB+MD=3+ (km)…………………(3分)
(km)…………………(3分)
方案二:如图①,作点M关于射线OE的对称点M′,则MM′=2ME,
连接AM′交OE于点P,PE∥AM,PE= 。
。
∵AM=2BM=6,∴PE=3 …………………(4分)
在Rt△DME中,
∵DE=DM·sin60°= ×
× =3,ME=
=3,ME= =
= ×
× ,
,
∴PE=DE,∴ P点与E点重合,即AM′过D点。…………(6分)
在线段CD上任取一点P′,连接P′A,P′M,P′M′,
则P′M=P′M′。
∵A P′+P′M′>AM′,
∴把供水站建在乙村的D点处,管道沿DA、DM线路铺设的长度之和最小,
即最小值为AD+DM=AM′= ………(7分)
………(7分)


方案三:作点M关于射线OF的对称点M′,作M′N⊥OE于N点,交OF于点G,
交AM于点H,连接GM,则GM=GM′
∴M′N为点M′到OE的最短距离,即M′N=GM+GN
在Rt△M′HM中,∠MM′N=30°,MM′=6,
∴MH=3,∴NE=MH=3
∵DE=3,∴N、D两点重合,即M′N过D点。
在Rt△M′DM中,DM= ,∴M′D=
,∴M′D= …………(10分)
…………(10分)
 在线段AB上任取一点G′,过G′作G′N′⊥OE于N′点,
在线段AB上任取一点G′,过G′作G′N′⊥OE于N′点,
连接G′M′,G′M,
显然G′M+G′N′=G′M′+G′N′>M′D
∴把供水站建在甲村的G处,管道沿GM、GD
线路铺设的长度之和最小,即最小值为
GM+GD=M′D= 。 …(11分)
。 …(11分)
综上,∵3+ <
< ,
,
∴供水站建在M处,所需铺设的管道长度最短。 …………(12分)
24.(08江苏扬州)(本题答案暂缺)26.(本题满分14分)
已知:矩形ABCD中,AB=1,点M在对角线AC上,直线l过点M且与AC垂直,与AD相交于点E。
(1)如果直线l与边BC相交于点H(如图1),AM= AC且AD=A,求AE的长;(用含a的代数式表示)
AC且AD=A,求AE的长;(用含a的代数式表示)
(2)在(1)中,又直线l 把矩形分成的两部分面积比为2:5,求a的值;
(3)若AM= AC,且直线l经过点B(如图2),求AD的长;
AC,且直线l经过点B(如图2),求AD的长;
(4)如果直线l分别与边AD、AB相交于点E、F,AM= AC。设AD长为x,△AEF的面积为y,求y与x的函数关系式,并指出x的取值范围。(求x的取值范围可不写过程)
AC。设AD长为x,△AEF的面积为y,求y与x的函数关系式,并指出x的取值范围。(求x的取值范围可不写过程)
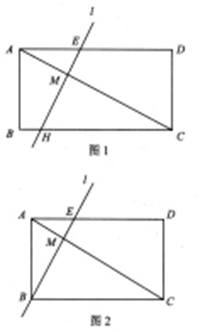
23.(08江苏盐城)(本题答案暂缺)28.(本题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ▲ ,数量关系为 ▲ .
 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC= ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com