
7. 2007年10月24日18时05分,嫦娥一号绕月卫星发射成功。是中国科学院院士、中国探月工程首席科学家欧阳自远在此间举行的一次学术会上介绍说,科学技术的发展,将使月球上两种资源给地球能源问题带来希望;一是月球的太阳能;二是月壤中气体,如氢、氦、氖、氩、氮等资源。下列有关氮元素的叙述不正确的是 ( )
A.硝化细菌可将氨态氮转化为硝态氮,有利于植物对氮元素的吸收
B.反硝化细菌属于分解者,在无氧条件下可将氨态氮转化为氮气中耕松土可防止氮元素的流失
C.土壤中的含氧量将影响氮元素的吸收
D.圆褐固氮菌可独立固氮,属于异养型生物
6. 生物体内基本组成单位相同的一组物质是 ( )
A.植物的纤维素和生长素 B.动物的糖元和抗原
C.人的胰岛素和雌激素 D.细菌的质粒和T2噬菌体的遗传物质
5. 雄性羚羊角或犀牛角是治疗创伤的中药方剂中用量极少的成分,但是缺少这味药,疗效将大大下降甚至无效。已知动物的角主要是由死亡细胞的角化(变性)蛋白质组成。则羚羊角等的有效成分最可能是 ( )
A.特殊活性蛋白质 B.DNA C.微量元素 D.大量元素
4. 经测定某化合物含C、H、O、N、S等元素,该化合物不可能具有的一项功能是 ( )
A.用于基因工程获得黏性末端
B.用于动物细胞培养时制备细胞悬浮液
C.与核糖体结合作为翻译的直接模板
D.与抗原发生特异性结合
3. 一般说来,每100克蛋白质平均含氮16克,这些氮主要存在于蛋白质的 ( )
A.-CO-NH- B.游离的氨基 C.游离的羧基 D.R基
2. 牛通过吃草获得化合物和元素,那么,牛和草体内的各种化学元素 ( )
A.种类差异很大,含量大体相同 B.种类和含量差异都很大
C.种类和含量都是大体相同的 D.种类大体相同,含量差异很大
1. 在缺硼的土壤中最适宜种植的作物是 ( )
A.小麦 B.玉米 C.甘蔗 D.水稻
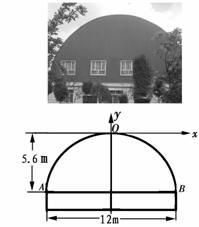
91.(08新疆自治区24题)(10分)某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.
(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
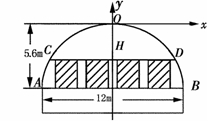
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
 (08新疆自治区24题解析)24.(10分)解:(1)设抛物线的表达式为
(08新疆自治区24题解析)24.(10分)解:(1)设抛物线的表达式为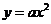 1分
1分
点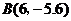 在抛物线的图象上.
在抛物线的图象上.
∴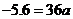
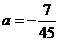 ······························································ 3分
······························································ 3分
∴抛物线的表达式为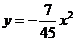 ············································································· 4分
············································································· 4分
(2)设窗户上边所在直线交抛物线于C、D两点,D点坐标为(k,t)
已知窗户高1.6m,∴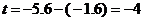 ··························································· 5分
··························································· 5分
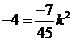
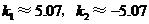 (舍去)············································································ 6分
(舍去)············································································ 6分
∴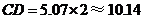 (m)·············································································· 7分
(m)·············································································· 7分
又设最多可安装n扇窗户
∴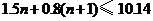 ····················································································· 9分
····················································································· 9分
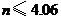 .
.
答:最多可安装4扇窗户.···················································································· 10分
(本题不要求学生画出4个表示窗户的小矩形)
90.(08四川自贡26题)抛物线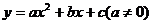 的顶点为M,与
的顶点为M,与 轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于
轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于 的一元二次方程
的一元二次方程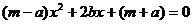 有两个相等的实数根。
有两个相等的实数根。
(1)判断△ABM的形状,并说明理由。
(2)当顶点M的坐标为(-2,-1)时,求抛物线的解析式,并画出该抛物线的大致图形。
(3)若平行于 轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与
轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与 轴相切,求该圆的圆心坐标。
轴相切,求该圆的圆心坐标。
(08四川自贡26题解析)解:(1)令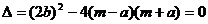
得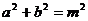
由勾股定理的逆定理和抛物线的对称性知
△ABM是一个以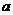 、
、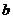 为直角边的等腰直角三角形
为直角边的等腰直角三角形
(2)设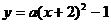
∵△ABM是等腰直角三角形
∴斜边上的中线等于斜边的一半
又顶点M(-2,-1)
∴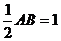 ,即AB=2
,即AB=2
∴A(-3,0),B(-1,0)
将B(-1,0) 代入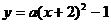 中得
中得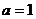
∴抛物线的解析式为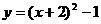 ,即
,即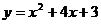
图略
(3)设平行于 轴的直线为
轴的直线为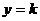
解方程组错误!不能通过编辑域代码创建对象。
得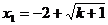 ,
,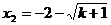 (
(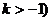
∴线段CD的长为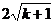
∵以CD为直径的圆与 轴相切
轴相切
据题意得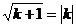
∴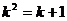
解得 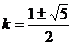
∴圆心坐标为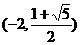 和
和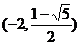
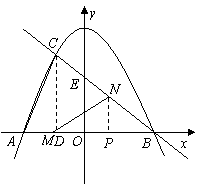
89.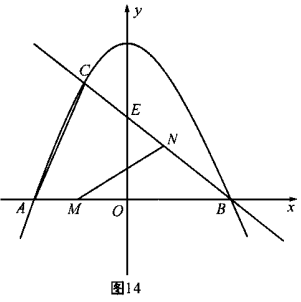 (08四川巴中30题)(12分)30.已知:如图14,抛物线
(08四川巴中30题)(12分)30.已知:如图14,抛物线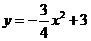 与
与 轴交于点
轴交于点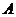 ,点
,点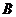 ,与直线
,与直线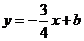 相交于点
相交于点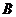 ,点
,点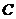 ,直线
,直线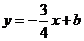 与
与 轴交于点
轴交于点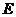 .
.
(1)写出直线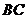 的解析式.
的解析式.
(2)求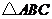 的面积.
的面积.
(3)若点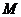 在线段
在线段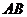 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从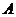 向
向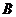 运动(不与
运动(不与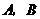 重合),同时,点
重合),同时,点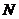 在射线
在射线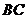 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从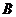 向
向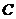 运动.设运动时间为
运动.设运动时间为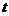 秒,请写出
秒,请写出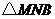 的面积
的面积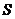 与
与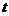 的函数关系式,并求出点
的函数关系式,并求出点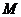 运动多少时间时,
运动多少时间时,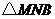 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
 (08四川巴中30题解析)解:(1)在
(08四川巴中30题解析)解:(1)在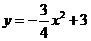 中,令
中,令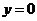
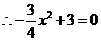
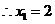 ,
,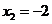
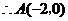 ,
,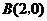 ··············································· 1分
··············································· 1分
又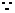 点
点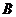 在
在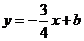 上
上
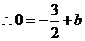
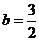
 的解析式为
的解析式为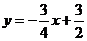 ·············································································· 2分
·············································································· 2分
(2)由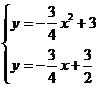 ,得
,得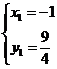
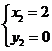 ···················································· 4分
···················································· 4分
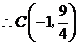 ,
,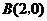
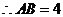 ,
,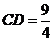 ······························································································· 5分
······························································································· 5分
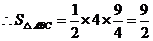 ························································································· 6分
························································································· 6分
(3)过点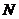 作
作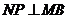 于点
于点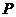
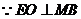
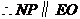
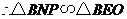 ······························································································· 7分
······························································································· 7分
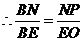 ·········································································································· 8分
·········································································································· 8分
由直线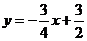 可得:
可得: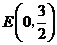
 在
在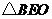 中,
中,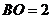 ,
,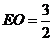 ,则
,则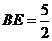
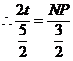 ,
,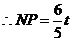 ······················································································· 9分
······················································································· 9分
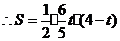
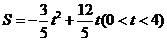 ···················································································· 10分
···················································································· 10分
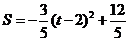 ····························································································· 11分
····························································································· 11分
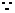 此抛物线开口向下,
此抛物线开口向下, 当
当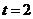 时,
时,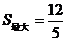
 当点
当点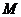 运动2秒时,
运动2秒时,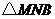 的面积达到最大,最大为
的面积达到最大,最大为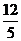 .···························· 12分
.···························· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com